2. Выписать все элементы множества  , где
, где 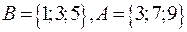
Решение.
1 Подмножества множества 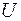 могут содержать от нуля до четырёх элементов (включая пустое множество и множество
могут содержать от нуля до четырёх элементов (включая пустое множество и множество 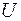 ). Будем выписывать подмножества в порядке возрастания количества элементов. Учтём, что пустое множество является подмножеством любого множества, кроме того, любое множество является подмножеством самого себя.
). Будем выписывать подмножества в порядке возрастания количества элементов. Учтём, что пустое множество является подмножеством любого множества, кроме того, любое множество является подмножеством самого себя.
Имеем:
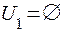 ;
;
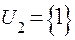 ;
;
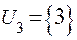 ;
;
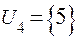 ;
;
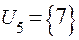 ;
;
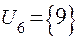 ;
;
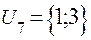 ;
;
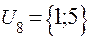 ;
;
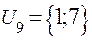 ;
;
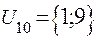 ;
;
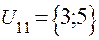 ;
;
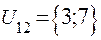 ;
;
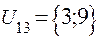 ;
;
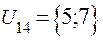 ;
;
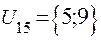 ;
;
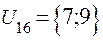 ;
;
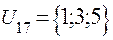
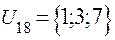 ;
;
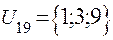 ;
;
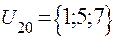 ;
;
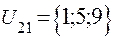 ;
;
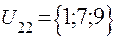 ;
;
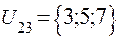 ;
;
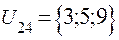 ;
;
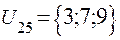 ;
;
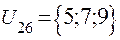 ;
;
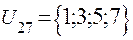 ;
;
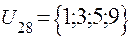 ;
;
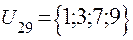 ;
;
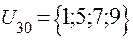 ;
;
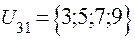 ;
;
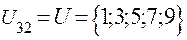 .
.
2 Будем искать множество 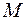 , выполняя операции последовательно.
, выполняя операции последовательно.
1) Множество 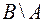 состоит из всех элементов множества
состоит из всех элементов множества 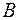 , которые не принадлежат множеству
, которые не принадлежат множеству 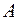 . Имеем:
. Имеем: 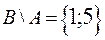 ;
;
2) Множество 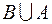 состоит из всех элементов, принадлежащих хотя бы одному из множеств
состоит из всех элементов, принадлежащих хотя бы одному из множеств 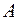 или
или 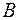 . Имеем:
. Имеем:
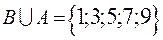 .
.
3) Множество 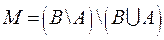 состоит из всех элементов множества
состоит из всех элементов множества 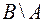 , которые не принадлежат множеству
, которые не принадлежат множеству 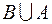 .
.
Видим, что, М – пустое множество.
2. Доказать методом включений тождество:
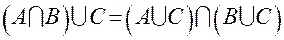 .
.
Решение.
Необходимо доказать выполнение включений:
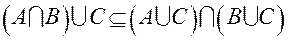 и
и 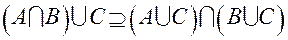 .
.
1. Выберем произвольный элемент 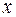 множества
множества 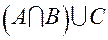 . По определению операции объединения множеств
. По определению операции объединения множеств 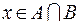 или
или 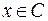 .
.
Если 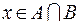 , то по определению операции пересечения множеств
, то по определению операции пересечения множеств 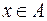 и
и 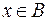 .
.
Так как 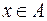 , то
, то 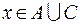 ; так как
; так как 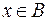 , то
, то 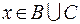 , следовательно,
, следовательно, 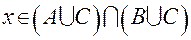 .
.
Если 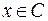 , то
, то 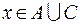 и
и 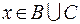 , и, таким образом,
, и, таким образом, 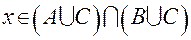 .
.
Поскольку элемент 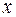 множества
множества 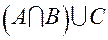 был выбран произвольно, можно утверждать, что любой элемент этого множества содержится в
был выбран произвольно, можно утверждать, что любой элемент этого множества содержится в 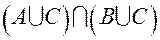 , то есть
, то есть 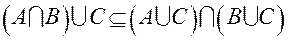 .
.
2. Выберем произвольный элемент 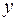 из множества
из множества
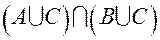 .
.
По определению операции пересечения множеств 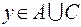 и
и 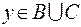 .
.
Так как 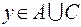 , то
, то 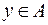 или
или 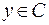 ; так как
; так как 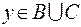 , то
, то 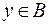 или
или 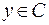 . Таким образом,
. Таким образом, 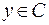 или
или 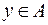 и
и 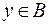 .
.
Если 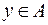 и
и 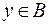 , то
, то 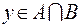 , а, следовательно,
, а, следовательно, 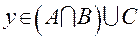 ; если
; если 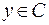 , то также имеем
, то также имеем 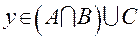 .
.
Поскольку элемент 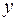 множества
множества 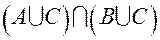 был выбран произвольно, можно утверждать, что любой элемент этого множества содержится в
был выбран произвольно, можно утверждать, что любой элемент этого множества содержится в 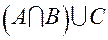 , то есть
, то есть 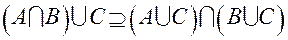 .
.
3. Из пунктов 1 и 2 следует, что 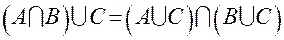 .
.
Доказано.
2. «Отображения множеств».
 2015-06-28
2015-06-28 1869
1869








