Часто элементы разных множеств связаны различными отношениями. Отношение является фундаментальным понятием математики, так же, как и понятие множества. Отношение используется для обозначения связи между объектами или понятиями, при этом отношение может быть многоместным.
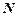 -местное (
-местное (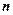 -арное) отношение на множестве
-арное) отношение на множестве 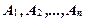 это любое подмножество декартова произведения
это любое подмножество декартова произведения 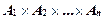 .
.
Обычно отношение в отличие от соответствия, которое обозначается буквой 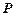 , обозначается буквой
, обозначается буквой 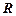 , но записи аналогичны.
, но записи аналогичны.
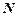 -местное отношение обозначается как
-местное отношение обозначается как 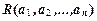 или
или 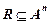 . Говорят, что
. Говорят, что 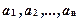 находятся в отношении
находятся в отношении 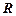 , если
, если 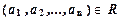 .
.
Пусть, например, V – множество всех точек плоскости, а L – множество всех прямых этой плоскости. Отношение 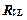 «прямые
«прямые 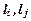 пересекаются в точке
пересекаются в точке 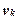 » – трехместное отношение, определенное на множестве
» – трехместное отношение, определенное на множестве 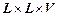 . Оно является множеством всех троек
. Оно является множеством всех троек 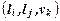 , таких, что
, таких, что 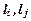 пересекаются в точке
пересекаются в точке 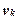 .
.
При 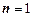 отношение
отношение 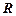 называется одноместным или унарным и является подмножеством множества
называется одноместным или унарным и является подмножеством множества 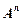 , то есть одноместное отношение – это просто подмножество
, то есть одноместное отношение – это просто подмножество 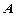 . Такие отношения еще называют признаками:
. Такие отношения еще называют признаками: 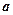 обладает признаком
обладает признаком 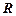 , если
, если 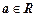 и
и 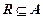 . Свойства одноместных отношений – это свойства подмножеств
. Свойства одноместных отношений – это свойства подмножеств 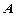 , поэтому для случая
, поэтому для случая 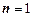 термин отношение употребляется редко. Примером унарного отношения является равенство типа
термин отношение употребляется редко. Примером унарного отношения является равенство типа 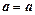 , в быту это самообслуживание.
, в быту это самообслуживание.
При 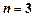 отношение Р называется трехместным или триарным, или тернарным. Примером трехместного отношения является множество троек нападающих в хоккейной команде. Каждый из нападающих находится в этом отношении со всеми теми игроками, с которыми он играет в одной тройке (хотя один нападающий может находиться в отношении и с другими игроками, находящимися на льду, но в составе тройки он связан обязанностями, отличающимися от его отношений с защитниками). Примером трехместного отношения является также арифметическая операция с тремя величинами
отношение Р называется трехместным или триарным, или тернарным. Примером трехместного отношения является множество троек нападающих в хоккейной команде. Каждый из нападающих находится в этом отношении со всеми теми игроками, с которыми он играет в одной тройке (хотя один нападающий может находиться в отношении и с другими игроками, находящимися на льду, но в составе тройки он связан обязанностями, отличающимися от его отношений с защитниками). Примером трехместного отношения является также арифметическая операция с тремя величинами 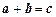 .
.
Наиболее известны отношения при 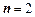 , которые называются двухместными или бинарными отношениями, отражающими связь между двумя объектами. Для этих отношений, если
, которые называются двухместными или бинарными отношениями, отражающими связь между двумя объектами. Для этих отношений, если 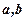 находятся в отношении
находятся в отношении 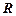 , это записывается как
, это записывается как 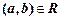 или
или 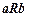 .
.
Бинарное отношение 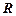 на множестве
на множестве 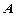 – это всякое подмножество декартова произведения
– это всякое подмножество декартова произведения 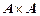 . Обозначается
. Обозначается 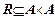 или
или 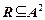 .
.
Диагональ множества 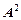 – отношение
– отношение 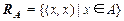 .
.
Если 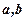 не находятся в отношении
не находятся в отношении 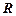 , это записывается как
, это записывается как 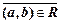 или
или 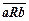 .
.
 2015-06-28
2015-06-28 1781
1781
