Пример 2.6

Даносоответствие между 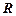(осью абсцисс) и 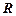(осью ординат) в виде круга 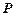радиуса 1 с центром в точке (3, 2) (рис. 2.4), то есть в виде множества пар действительных чисел 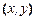, удовлетворяющих соотношению .

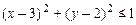Образом в данном соответствии для числа 4 (ось абсцисс) является единственное число 2 (ось ординат), образом числа 3 является уже отрезок [1, 3] оси ординат.

Прообразом отрезка [1, 3] (ось ординат) является отрезок [2, 4] (ось абсцисс).

Данное соответствие не является функциональным, поскольку для такого соответствия необходимо, чтобы образом любого элемента из множества 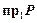являлся единственный элемент из множества 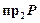. Здесь множество 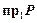это множество всех действительных чисел 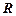(ось абсцисс), каждому из которых может соответствовать не единственный образ из множества 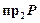– множества всех действительных чисел 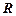(ось ординат).

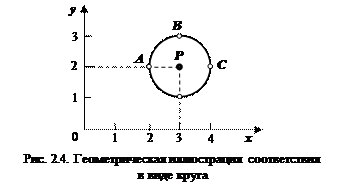
Примером функционального соответствия на том же рис. 2.4 могут служить дуги окружности, координаты которых каждой единственной точке на оси абсцисс ставят в соответствие единственную точку на оси ординат. В частности это могут быть дуг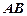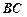и , или .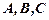

Отметим, что в общем случае для задания соответствия необходимо указать не только множество 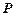, но и множества 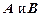, то есть указать, подмножеством какого прямого произведения является 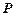. В данном примере тот же круг 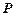задает и другое соответствие: между отрезком [2, 4] и отрезком [1, 3]. При этом по некоторым свойствам соответствия 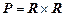и 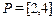× 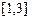отличаются: так второе соответствие в отличие от первого всюду определено и сюръективно, то есть 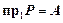и 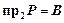. Учитывая это, соответствие необходимо было бы определять как тройку множеств 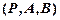, и тогда не было бы необходимости оговариваться, что один круг может задавать два соответствия, поскольку это и так было бы ясно из-за различия троек 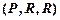и 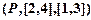. Однако такие оговорки обычно делаются редко, так как либо множества 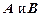ясны из контекста, либо различия в из выборе не влияют на исследуемые свойства соответствия. Поэтому определение соответствия через тройку множеств здесь использоваться не будет.