Нахождение корней уравнения. Подбор параметра. Поиск решения.
Персональное задание выбрать по номеру варианта в “Приложение 2 ”.
Задание 2.1
P Открыть новый лист;
P В Приложении 2 выбрать функцию F(x), построить таблицу 1 значений функции и точечный график.
P Используя редактор формул, вставить на лист функцию F(x), номер варианта;
P В таблице 1 значения переменной X заполнять, используя заполнить/прогрессия;
P в таблице 1 выделить цветом строки, в которых находятся приблизительные значения корней функции;
P переименовать ярлык рабочего листа на название функции;
Задание 2.2
Найти приближенное значение корня уравнения F(x)=0 следующими способами:
1. по графику;
2. используя инструмент ПОДБОР ПАРАМЕТРА;
3. используя инструмент ПОИСК РЕШЕНИЯ.
Результаты вывести в таблицу.
Задание 2.2.1
ü Создайте таблицу 2, в которую внесите приближенное значение корня (корней) и соответствующее ему значение функции F(x), полученные по графику функции (или по таблице).
ü Вычислите приближенное значение корня (корней), используя инструмент Подбор параметра (Данные/Работа с данными/Анализ “что если”).
ü Вычислить приближенное значение корня (корней), используя инструмент Поиск решения. По результатам вычисления распечатать отчет.
Если в меню отсутствует пункт Поиск решения, то установите его: меню / Файл / Параметры / Надстройки / Поиск решения / Применить / флажок Поиск решения.
ü Установить параметры вычисления:
предельное число итераций: 50;
точность вычислений (сходимость): 0,0001;
максимальное время: 50сек.;
относительная погрешность 0,000001.
Задание 2.2.2
Используя инструмент для вставки формул, написать в общем виде уравнение параболы y=ax3+bx2+cx+d;
С помощью инструмента Поиск решения вычислить значения коэффициентов a, b, c, d, при которых точка M(x1; y1) принадлежит параболе. Произвольные значения координат точки М задать самостоятельно.
Проанализировать результат.
Используя инструмент для вставки формул, написать полученное уравнение параболы, используя Редактор формул.
Приложение №1
ВАРИАНТЫ ЗАДАНИЙ
| № варианта | xmin | xmax | x1 | x2 | h | a | b | F1 | F2 | F3 |
| 1. | -12 | -6 | 0, 5 | -5 | Y=2cos(X-3) | Y=|X+4|1/2 | Y=(X+2)/2 | |||
| 2. | -9 | -3 | 0,2 | -7 | Y=cos(X+3) | Y=X+4 | Y=3|X+4|1/2 | |||
| 3. | -8 | -4 | 0,5 | -2 | Y=-X+5 | Y=-(X+1)3/3 | Y=X-11 | |||
| 4. | -7 | -5 | Y=cos(X)+1 | Y=-X+2 | Y=ln(X/6)-4 | |||||
| 5. | -5 | 0,2 | -3 | Y=sin(0,5X-2) | Y=2X-8 | Y=2*|2X|1/2 | ||||
| 6. | -9 | 0,5 | -6 | Y=(X/4-1)3 | Y=X-1 | Y=2*|X+7|1/2 | ||||
| 7. | -6 | -4 | 0,25 | -1 | Y=-(X/3-1)3 | Y=2*|X-5|1/2+2 | Y=2(X+2) | |||
| 8. | -9 | -2 | 0,2 | -9 | -7 | Y=-2X | Y=2*|-2X|1/2 | Y=8 | ||
| 9. | -10 | 0,25 | -4 | Y=-2cos(X) | Y=-X-2 | Y=ln(X-5)-8 | ||||
| 10. | -10 | -7 | 0,5 | -8 | Y=sin(X+7)+3 | Y=3|X+6|1/2 | Y=-X+12 | |||
| 11. | -8 | -3 | 0,2 | -5 | Y=sin(X+3) | Y=|X+3|1/2 | Y=X/2 | |||
| 12. | -10 | -3 | 0,25 | -2 | Y=cos(X+3) | Y=X+4 | Y=3|X+4|1/2 | |||
| 13. | -10 | -4 | 0,25 | Y=-X+5 | Y=-(X+1)3/3 | Y=X-11 | ||||
| 14. | -7 | -5 | Y=cos(X)+1 | Y=-X+2 | Y=ln(X/6)-4 | |||||
| 15. | -5 | 0,2 | -3 | Y=sin(0,5X-2) | Y=2X-8 | Y=2*|2X|1/2 | ||||
| 16. | -8 | 0,25 | -6 | Y=(X/4-1)3 | Y=X-1 | Y=2*|X+7|1/2 | ||||
| 17. | -8 | -4 | 0,2 | -8 | Y=-(X/3-1)3 | Y=2*|X-5|1/2+2 | Y=2(X+2) | |||
| 18. | -9 | -2 | 0,25 | -4 | -1 | Y=-2X | Y=2*|-2X|1/2 | Y=8 | ||
| 19. | -7 | 0,2 | -1 | Y=-2cos(X) | Y=-X-2 | Y=ln(X-5)-8 | ||||
| 20. | -10 | -7 | 0,5 | -6 | Y=sin(X+7)+3 | Y=3|X+6|1/2 | Y=-X+12 |
| № варианта | xmin | xmax | x1 | x2 | h | a | b | F1 | F2 | F3 |
| 21. | -10 | -3 | 0,5 | -7 | Y=sin(2X-3)-3 | Y=|X+3|1/3-2 | Y=X2/2-3x | |||
| 22. | -9 | -3 | 0,25 | -3 | Y=cos(X+3) | Y=X+4 | Y=3|X+4|1/2 | |||
| 23. | -9 | -4 | 0,25 | Y=-X+5 | Y=-(X+1)3/3 | Y=X-11 | ||||
| 24. | -7 | -5 | Y=cos(X)+1 | Y=-X+2 | Y=ln(X/6)-4 | |||||
| 25. | -8 | 0,25 | -5 | Y=2sin(0,8X-2) | Y=X2-8 | Y=2*|2X|1/2 | ||||
| 26. | -9 | 0,5 | -7 | Y=(X/4-1)3 | Y=X-1 | Y=2*|X+7|1/2 | ||||
| 27. | -8 | -4 | 0,25 | Y=-(X/3-1)3 | Y=2*|X-5|1/2+2 | Y=2(X+2) | ||||
| 28. | -10 | -2 | 0,25 | -9 | -3 | Y=-2X | Y=2*|-2X|1/2 | Y=8 | ||
| 29. | -5 | 0,25 | -4 | Y=-2cos(X) | Y=-X-2 | Y=ln(X-5)-8 | ||||
| 30. | -10 | -7 | 0,5 | -8 | Y=sin(X+7)+3 | Y=3|X+6|1/2 | Y=-X+12 | |||
| 31. | -7 | 0,25 | -5 | Y=sin(0,5X-2) | Y=2X-8 | Y=2*|2X|1/2 | ||||
| 32. | -9 | -5 | 0,25 | -2 | Y=4-(X/3-1)3 | Y=2*|X-5|1/2+3 | Y=2(X-3) |
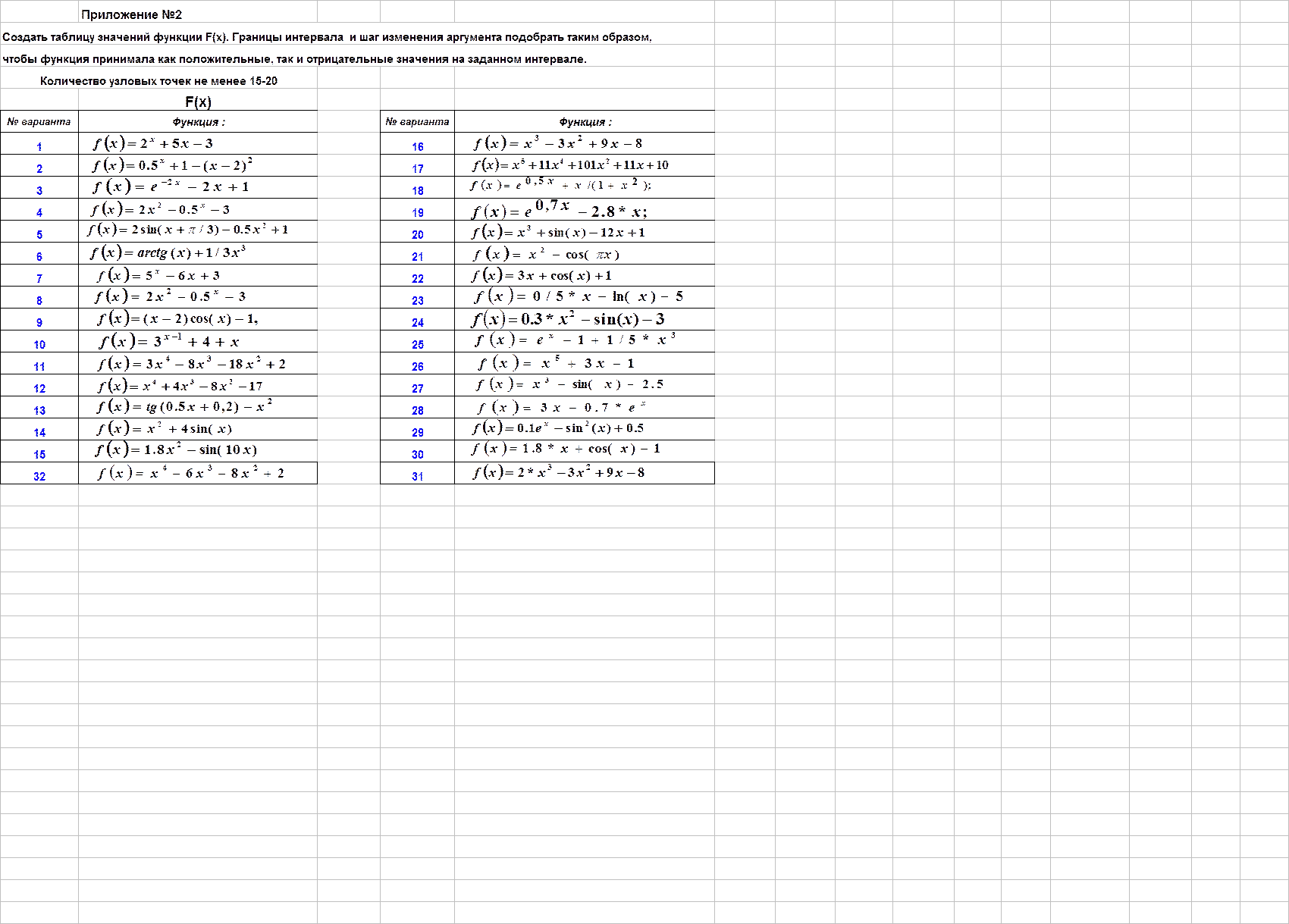
 2015-06-28
2015-06-28 1089
1089







