Рассмотрим зависимость от расстояния энергии притяжения частиц – молекулярной составляющей расклинивающего давления. Из сил Ван – дер – Вальса наиболее универсальными и существенными силами притяжения являются лондоновские силы дисперсионного взаимодействия. Дисперсионное взаимодействие слабо экранируется, и поэтому взаимодействие между частицами легко определить суммированием взаимодействий между молекулами и атомами в обеих частицах, например, с помощью интегрирования. Такой приближенный расчет в предположении аддитивности межмолекулярных (межатомных) взаимодействий был проведен де Буром и Гамакером. Для вывода уравнения энергии молекулярного притяжения между частицами воспользуемся уравнением энергии притяжения одной молекулы.
Uадс = -πCn/(6х3) (14)
где С – константа, зависящая от природы взаимодействующих тел;
n – число молекул (атомов) в единице объема частиц.
Рис.2 К выводу уравнения для энергии
Молекулярного притяжения пластинами
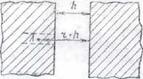
На рис. 2 показаны две взаимодействующие между собой пластины (как предполагается в упрощенном варианте теории ДЛФО). Предложим, что одна молекула (атом) А внутри левой пластины притягивается к правой пластине с энергией Uадс, рассчитываемой по приведенному уравнению (14). Расстояние х = r + h, где r – расстояние молекулы (атома) от поверхности левой пластины. Чтобы получить энергию молекулярного притяжения пластин, необходимо просуммировать энергии притяжения всех молекул (атомов) левой пластины с правой. Приращение энергии молекулярного притяжения, отнесенное к единице площади пластин, пропорционально приращению числа молекул (атомов) в цилиндре
(см. рис.2) с основанием, равным единице площади, т.е. ndr, или
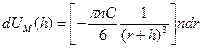 (15)
(15)
После интегрирования получим:
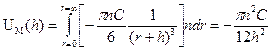 (16)
(16)
или
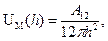
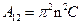 (17)
(17)
Из уравнения (17) видно, что энергия притяжения пластин обратно пропорциональна квадрату расстояния между ними. Это указывает на то, что энергия притяжения между пластинами (частицами) значительно медленнее уменьшается с расстоянием, чем энергия притяжения между атомами (молекулами), которая обратно пропорциональна расстоянию в шестой степени. Отсюда также следует, что частицы коллоидных систем взаимодействуют на более далеких расстояниях, чем атомы (молекулы).
Величина А12 в уравнении (17) называется константой Гамакера. Она учитывает природу взаимодействующих тел. Эта константа выражается в единицах измерения энергии и имеет значение порядка 10-19Дж. Вывод уравнения (17) проводился в предположении, что пластины находятся в вакууме. При наличии среды константа А12 в уравнении (17) заменяется на величину.
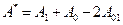 (18)
(18)
тогда
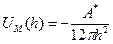 (19)
(19)
Где А1 и А0 – константы Гамакера для дисперсной фазы, состоящей из частиц (1) и дисперсной среды (0) соответственно; А01 – постоянная взаимодействия фазы и среды.
Чем сильнее взаимодействует фаза со средой, тем больше А01 и тем меньше А*, это значит, что уменьшаются силы притяжения между частицами.
Имея отдельные выражения для энергии отталкивания и энергии притяжения частиц, простым сложением получим общую энергию взаимодействия между двумя параллельными пластинами (частицами), приходящую на единицу площади. Для области малых потенциалов суммарная энергия взаимодействия равна:
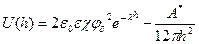 (20)
(20)
При больших потенциалов и расстояния между пластинами эта энергия определяется уравнением:
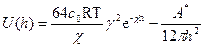 (21)
(21)
По более сложным уравнениям рассчитывают энергии взаимодействия сферических частиц.
Так, для двух сферических частиц одинакового радиуса r при расстоянии между центрами частиц R и минимальной ширине зазора между их поверхностями h = R – 2r (рис 3) проведенная Гемакером интегрирование молекулярных взаимодействий дало общее выражение энергии притяжения частиц:
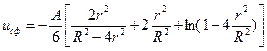 (22)
(22)
Подчеркнем, что величина uсф, как и А, имеет размерность энергии.
При большом расстоянии между центрами частиц R>>r (формула 22) разложения слагаемых в ряды:
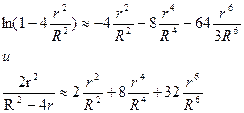
может быть приведена к виду, аналогичному выражению для взаимодействия между молекулами:
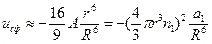 (23)
(23)
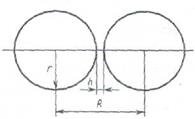 |
Рис.3 где n1 – число молекул в единице
объема частицы.
В другом крайнем случае, когда размер частиц значительно больше толщены зазора между ними: r >> h = R – 2r, основной вклад в выражение для uсф дает первое слагаемое в скобках, которое можно представить в виде
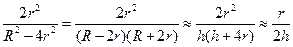
Следовательно,
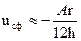 (24)
(24)
При взаимодействии двух сферических частиц, разделенной тонкой прослойкой дисперсионной среды, их энергия притяжения описывается выражением:
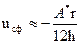
Таким образом, приближенное решение общего уравнения для сферических частиц с низким значением потенциала φδ при условии, что их радиус r значительно больше толщины диффузного слоя 1/æ, приводит к следующей формуле:
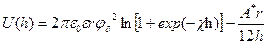 (25)
(25)
В соответствии с теорией ДЛФО соотношения (20), (21) и (25) определяют поведение дисперсных систем. Их устойчивость или скорость коагуляции зависят от знака и значения общей потенциальной энергии взаимодействия частиц. Положительная энергия отталкивания Uэ(h) с увеличением расстояния уменьшается по экспоненциальному закону, а отрицательная энергия притяжения Uм(h) обратно пропорциональна квадрату расстояния (рис. 4). В результате на малых расстояниях (при h→0 Uэ→соnst, Uм→ - ∞) и больших расстояниях (экспонента убывает значительно быстрее, чем степенная функция) между частицами преобладает энергия притяжения, а на средних расстояниях – энергия электростатического отталкивания. Первичный минимум отвечает непосредственному слипанию частиц (рис.4); а вторичный – их притяжению через прослойку среды (рис.34). Максимум на средних расстояниях характеризует потенциальный барьер, препятствующий слипанию частиц. Силы взаимодействия могут распространяться на расстояния до сотен нанометров, максимальное значение энергии достигает 10-2 Дж/м2 и более. Увеличению потенциального барьера способствует рост потенциала φδ при их малых значениях на поверхности частиц. Практика показывает, что уже при φδ≈ 20мВ возникает потенциальный барьер, обеспечивающий агрегативную устойчивость дисперсной системы.
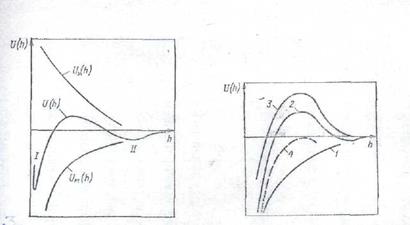 |
Рис.4 зависимость энергии электростатического отталкивания Uэ энергии молекулярного притяжения Uм и суммарной энергии взаимодействия частиц (пластин) от расстояния.
Рис. 5 потенциальные кривые для дисперсных систем с разной степенью и характером устойчивости.
Потенциальный барьер увеличивается и с уменьшением константы Гамакера А*.
Различают три наиболее характерных вида потенциальных кривых, отвечающих определенным состояниям устойчивости дисперсных систем (рис. 5). Кривая 1 на рис. 5 отвечает такому состоянию дисперсной системы, когда при любом расстоянии между частицами преобладает энергия притяжения над энергией отталкивания. Не меняет этого соотношения и тепловое движения частиц. При таком состоянии дисперсной системы наблюдается быстрая коагуляция с образованием агрегатов; в системах с жидкой и газообразной дисперсными фазами происходит коалесценция.
Кривая 2 указывает на наличие достаточно высокого потенциального барьера и вторичного минимума. В системе, находящейся в таком состоянии, происходит быстрая флокуляция частиц на расстояниях, соответствующих вторичному минимуму. Благодаря наличию потенциального барьера частицы во флоккулах не имеют непосредственного контакта и разделены прослойками среды. Очевидно, что такое состояние отвечает обратимости коагуляции. Пептизация возможна после устранения вторичного минимума или его уменьшения до значения меньше КбТ.
Кривая 3 отвечает состоянию системы с высоким потенциальным барьером при отсутствии вторичного минимума или при его глубине, меньшей тепловой энергии (КбТ). вероятность образования агрегатов частиц в таких условиях очень мала, и дисперсные системы обладают большой агрегативной устойчивостью.
 2015-06-28
2015-06-28 3880
3880
