Электростатическая составляющая расклинивающего давления

В теории ДЛФО принято, что давление отталкивания обусловлено только электростатическими силами, поэтому

dП_э = ρdφ (6)

где ρ – объемная плотность заряда в двойном электрическом слое;

φ – электрический потенциал двойного слоя.

Наиболее точное описание распределения объемной плотности заряда в двойном электрическом слое дает теория Штерна. Для упрощения вывода зависимости энергии отталкивания от расстояния предполагают, что при взаимодействии пластин происходит деформация только диффузной части двойного электрического слоя, и поэтому можно воспользоваться теорией Гуи – Чепмена. Ограничимся случаем, когда потенциал φ имеет малое значение, и его изменение следует уравнению:

φ_х = φ_δе^-æх (7)

где φ_δ – потенциал диффузной части двойного электрического слоя; æ- величина, обратная толщине диффузной части двойного слоя.

Если пластина находится на расстоянии h = 2x, на котором они не взаимодействуют (рис.1), то их двойные электрические слои не перекрываются и потенциалы в них снижаются практически до нуля. При сближении пластин их двойные электрические слои перекрываются и соотношение может быть применено только для области, близкой к поверхности пластин (1б). Принимают, что в середине расстояния между пластинами в результате взаимодействия их двойных слоев потенциал становится равным 2φ_х, т.е. распределение потенциала происходит в соответствии со сплошной кривой на (рис.1б).

Таким образом, для определения электростатической составляющей расклинивающего давления интегрирование уравнения (6) необходимо провести в пределах области снижения потенциала при отталкивании пластин, т.е. от 2φ_х до нуля:

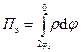(8)

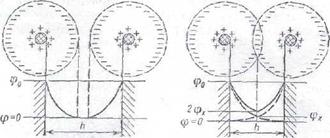а б

Рис.1. Схема распределения электрического потенциала между двумя одноименно заряженными частицами (пластинами) при неперекрытых (а) и перекрытых (б) двойных электрических слоях.

Сопоставляя уравнение Пуассона с соотношением Пуассона – Больцмана при малом значении потенциала:

d²φ/ dх² = - ρ/ε₀ ε

d²φ/ dх² = χ²φ

получим, что

ρ = - ε₀ ε χ²φ (9)

подставляя это выражение для ρ в (8), найдем:

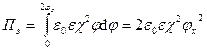(10)

Учитывая уравнение (9) и что h = 2х, получим зависимость электростатической составляющей расклинивающего давления от расстояния в области низких потенциалов:

П_э = 2ε₀εχ²φ_δ²е^-χh (11)

Если провести подобный вывод для области высоких потенциалов и больших расстояний между пластинами, то уравнение электростатической составляющей расклинивающего давления примет следующий вид:

П_э = 64с₀RTγ²е^-χh (12)

где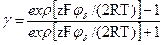

с₀ – концентрация противоионов в растворе; z – заряд противоионов; F – число Фарадея.

Следует отметить, что электростатическая составляющая расклинивающего давления в области малых потенциалов (11) сильно зависит от значения потенциала (пропорционально φ_δ²), с ростом же потенциала эта зависимость становится менее заметной.

При больших φ_δ потенциал перестает влиять на давление отталкивания.

Это можно объяснить тем, что с ростом потенциала одновременно увеличивается притяжение противоионов двойного электрического слоя к поверхности, эффективный заряд которой поэтому почти не изменяется.

Чтобы получить выражение для энергии электростатического отталкивания пластин, интегрируем уравнение (4) в пределах от h до ∞ после подстановки в него соотношения (11).

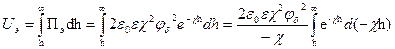(13)

Окончательно имеем:

U_э (h) = 2ε₀εχφ_δ²е^-χh (14)

При больших значениях потенциалов аналогично интегрирований уравнения (4) после подстановки соотношения (12) приводит к выражению:

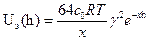(13)

Таким образом, энергия отталкивания пластин, как и электростатическая составляющая расклинивающего давления, возрастает с уменьшением расстояния h между ними по экспоненциальному закону.