Определение частоты опроса технологических параметров с помощью УВМ

Вопрос выбора необходимой частоты опроса технологических параметров с помощью УВМ возникает при создании АСУТП на стадии разработки технического задания (ТЗ).

Завышенная частота опроса ведет к усложнению системы дискретного контроля и повышению загрузки вычислительной части УВМ.

Заниженная частота опроса практически может свести к нулю результаты дискретного контроля, поскольку при этом невозможно проследить с необходимой точностью за изменением контролируемой величины.

Определим конкретный вид уравнения, используемого для определения интервала опроса в практически наиболее простом и распространенном случае ступенчатой экстраполяции, при которой о значении измеряемой величины в любой момент времени судят по измеренному значению величины в момент предыдущего отсчета (см. рис. 1), т.е.

при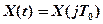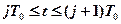

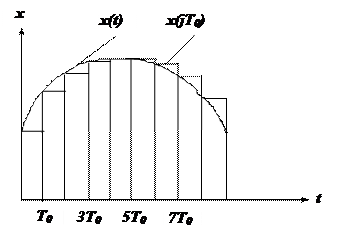(1)

где Т_о - период квантования (опроса) процесса Х(t) по времени

Рис. 1. Ступенчатая экстраполяция измеряемой величины

(2)

При экстраполяции возникает погрешность e(t) оценки текущего значения измеряемой величины, определяемая по формуле:

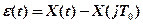
Погрешность e(t) является случайным процессом, особенностью которого является то, что равен нулю в момент начала каждого периода квантования (см. рис. 1).

Оценим среднюю квадратичную погрешность экстраполяции по методу (1) для случая, когда измеряемый процесс является стационарным.

Преобразуем уравнение (2), прибавив к правой части и отняв от нее величину математического ожидания процесса Мх:

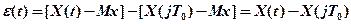
где Х(t) и Х(jT_o) - соответствующие центрированны

(3)

е процессы

Возведем левую и правую части выражения (3) в квадрат и будем рассматривать поведение функции e²(t) на отдельных интервалах времени 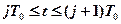или, если ввести новую переменную 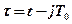,то на интервале .

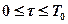Усредняя по множеству интервалов j, получим

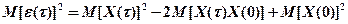
при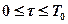

Используя понятия корреляционной функции и диспер

(7)

(6)

(5)

(4)

сия, в силу стационарности случайного процесса Х(t) будем иметь

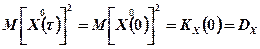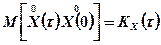где К_х и D_x - корреляционная функция и дисперсия случайного процесса.

С учетом (5) выражение (4) запишется в виде

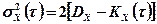
где 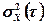- средняя квадратичная погрешность определения величины.

Выражение (6) не учитывает погрешность измерительного тракта (погрешность датчика) 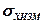. С ее учетом выражение для 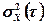примет вид

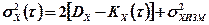
Из (7) следует, что средняя квадратичная погрешность 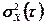является функцией времени t, т.е. меняется в пределах периода квантования. В моменты времени замера, т.е. при 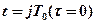эта погрешность является минимальной, равной погрешности измерительного тракта. Максимальное значение средняя квадратичная погрешность приобретает при экстраполяции в момент, пред

(9)

(8)

шествующий следующему замеру величины Х(t) при t = Т₀

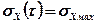
Частота опроса определяется по величине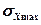

При t= Т_о уравнение (7) принимает вид

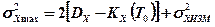
Формула (9) определяет период Т_о опроса датчика величины Х(t) по заданной погрешности ее определения 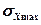, известной погрешности датчика 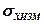и известной корреляционной функции процесса.