Решение

1) Найдем векторы 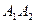и :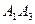

.

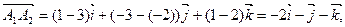
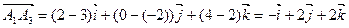Найдем длины этих векторов, т.е. длины ребер 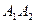и :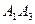

.

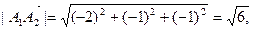
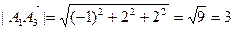2) Скалярное произведение векторов 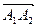и 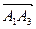найдем по формуле (3):

,

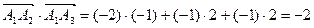косинус угла между этими векторами – по формуле:

.

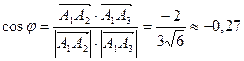Следовательно, φ – тупой угол, равный 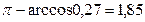рад с точностью до 0,01. Это есть искомый угол между ребрам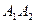и и .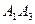

7. Вектор-столбец

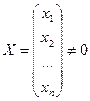
называется собственным вектором квадратной матрицы А n -го порядка, соответствующим собственному значению λ, если он удовлетворяет матричному уравнению 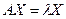или .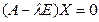

Здесь Е – единичная матрица n -го порядка, 0 – нулевой вектор-столбец. При условии, что вектор 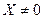, получаем характеристическое уравнение для определения собственных значений λ:

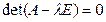(6)

Координаты собственного вектора 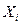, соответствующего собственному значению 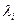, являются решением системы уравнений:

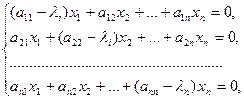(7)

Собственный вектор определяется до постоянного множителя.

Пример 5. Определить собственные значения и собственные векторы матрицы

.

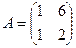Решение.

Характеристическое уравнение для данной матрицы имеет вид (6):

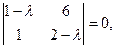или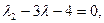

откуда следует, что матрица А имеет два собственных значения 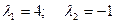. Собственный вектор Х₁, соответствующий 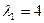, определяется из системы уравнений вида (7):

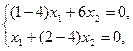или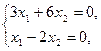

которая сводится к одному уравнению 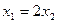. Полагая 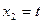, получаем решение в виде 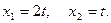Следовательно, первый собственный вектор есть .

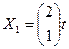Второй собственный вектор Х₂ , соответствующий собственному значению 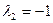, определяется из системы уравнений вида (7):

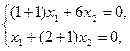
Эта система уравнений также сводится к одному уравнению 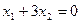; полагая 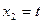, получаем решение в виде 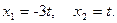Следовательно, первый собственный вектор есть .

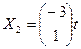Таким образом, матрица А имеет два собственных различных значения 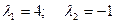и два собственных вектора, равных 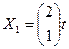и .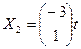

Контрольные вопросы

1. Что называется вектором?

2. Какие операции над векторами можно выполнять?

3. Дайте определение координаты вектора.

4. Что называется модулем вектора?

5. Дайте определение направляющим косинусам вектора.

6. Что называется проекцией вектора на ось?

7. Дайте определение скалярного произведения векторов.

8. Сформулируйте свойства скалярного произведения векторов.

9. С помощью каких формул можно вычислить скалярное произведение векторов?

10. Приведите формулы вычисления длины вектора и угла между векторами в координатной форме.

11. Сформулируйте условие ортогональности двух векторов.

12. Дайте определение векторного произведения векторов.

13. Сформулируйте свойства векторного произведения векторов.

14. Сформулируйте условие коллинеарности двух векторов.

15. Коллинеарны ли векторы 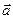и 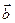, если коллинеарны векторы 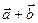и ?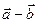

16. Докажите, что векторное произведение не изменится, если к одному из множителей прибавить вектор, коллинеарный другому множителю.

17. Чему равно векторное произведение противоположных векторов?

18. Равносильны ли равенства 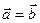и ?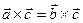

19. Дайте определение смешанного произведения векторов.

20. Сформулируйте условие компланарности векторов.

21. Докажите, что для любых заданных векторов 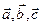векторы 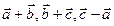компланарны.

22. Покажите, что объем параллелепипеда, построенного на диагоналях граней данного параллелепипеда, равен удвоенному объему данного параллелепипеда.

23. Дайте геометрическое построение разложения вектора 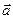на два компланарных с ним слагаемых, если известны:

а) длина и направление одного слагаемого;

б) направление обоих слагаемых;

в) направление одного и длина другого слагаемого.

Исследовать, когда разложение возможно, сколько имеет решений, если ни одно из слагаемых не параллельно .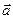

24. Дайте определение линейного оператора.

25. Дайте определение собственного вектора линейного оператора.

26. Дайте определение собственных значений линейных операторов.

27. Что называется линейным пространством?

28. Что называется Евклидовым пространством?

29. Дайте определение ортогональной системы векторов.