Решение. Примерами элементов отношения R могут быть векторы (a,c), (c,d)

Примерами элементов отношения R могут быть векторы (a,c), (c,d)... или цепочки ac, cd, bd..., такие, в которых на первом месте стоит буква, встречающаяся в латинском алфавите раньше по сравнению с буквой, стоящей на втором месте.

Отношение R является подмножеством множества M²:

M² = {aa, ab, ac,...,dd}, из которого элементы отбираются в соответствии со следующей процедурой R = {xy | x "меньше" y}.

R = {ab, ac, ad, bc, bd, cd}.

Отношения любой арности можно задать одним из способов задания множеств (перечисление элементов, порождающая процедура, характеристические признаки). Кроме того, бинарные отношения можно задавать:

· с помощью матрицы смежности – квадратной матрицы, столбцы и строки которой обозначены элементами несущего множества, а элементы имеют следующие значения:

;

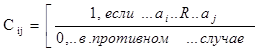· с помощью ориентированного графа – элементы несущего множества M изображаются на плоскости в виде вершин графа (точки с обозначением рядом элементов несущего множества), а затем вершины, пары которых входят в множество R, соединяются с помощью стрелок(дуг) (начинается стрелка в первом элементе пары, заканчивается – во втором); число таких стрелок равно числу элементов в множестве R.

Для каждого бинарного отношения R можно построить обратное отношение R^-1 (читается: R в степени минус один), поменяв местами в каждом элементе R проекции векторов.

Отношение Q обратно отношению R тогда и только тогда, когда для каждой пары из R выполняется условие:

x R y следует y Q x

1.7 Свойства бинарных отношений

1 Рефлексивность

Отношение R рефлексивно (обладает свойством рефлексивности), если для любого элемента х Î М установлено отношение х R х (на главной диагонали матрицы смежности – единицы); отношение R антирефлексивно, если ни для одного элемента х не установлено такого отношения (на главной диагонали матрицы смежности – нули); в других случаях (на главной диагонали есть и нули и единицы) говорят "отношение R не рефлексивно".

Таким образом, при установлении этого свойства отношения возможны следующие варианты: рефлексивно, не рефлексивно, антирефлексивно.

2 Симметричность

Отношение R называется симметричным, если для любого элемента этого отношения (х, y) в множестве R есть соответствующая пара – (y, x). Другими словами, если отношение R симметрично, то для каждой пары элементов несущего множества это отношение или установлено в обе стороны или не установлено вообще; отношение R называется антисимметричным, если приведенное выше условие выполняется только для случаев, когда x = y; отношение R называют несимметричным в остальных случаях. Таким образом, при установлении этого свойства отношения возможны следующие варианты: симметрично, несимметрично, антисимметрично.

Матрица смежности симметричного отношения симметрична относительно главной диагонали. Для симметричного отношения всегда выполняется равенство R = R^-1 (симметричное отношение и обратное ему отношение совпадают).

3 Транзитивность

Отношение R называется транзитивным, если среди множества его элементов для пары элементов вида (x, y), (y, z) всегда можно найти элемент (x, z). Другими словами, если на графе отношения из вершины x в вершину z, двигаясь по стрелкам, можно прийти через промежуточную вершину y, то для отношения, обладающего свойством транзитивности обязательно должен быть и прямой путь.

Если для рассматриваемого отношения имеется нарушение приведенного выше условия хотя бы в одном случае, то такое отношение не транзитивно.

Таким образом, при установлении этого свойства отношения возможны следующие варианты: транзитивно, не транзитивно.

1.8 Операции с бинарными отношениями

Поскольку бинарные отношения – это множества, для них определены рассмотренные выше операции над множествами (объединение, пересечение, разность, дополнение). Необходимо заметить:

· для бинарного отношения R универсальным множеством W всегда будет квадрат несущего множества М, т.е операция "дополнение R " всегда определена;

· при выполнении других операций результат будет корректным в том случае, если отношения построены на общем несущем множестве.

Операция прямое произведение при ее формальном применении к двум отношениям в результате даст отношение арности 4. Естественно потребовать, чтобы при выполнении этой операции арность результата не изменялась. Это достигается применением свойства транзитивности при выполнении операции перемножения отношений.

Пример: Пусть на несущем множестве M={a, b, c, d} заданы два бинарных отношения: R = {ab, ac, ad} и Q = {ac, ad, cd}. Произведением этих отношений будет также бинарное отношение S, элементы которого являются подмножеством элементов, полученных в результате формального перемножения множеств R и Q (из всего множества четырехсимвольных цепочек необходимо отобрать только те, у которых средние элементы одинаковы (при записи средние элементы опускаются):

S = R ´ Q = {accd, dccd} = {ad, dd}.

Примечание. Для более эффективного выполнения операции аналитического перемножения отношений нет необходимости перечислять все четырехсимвольные цепочки; нужно выбирать только те комбинации, у которых второй символ элемента первого отношения совпадает с первым символом элемента второго отношения.

Операцию прямое произведение отношений для двух отношений можно выполнить графически (на графах перемножаемых отношений) по следующему алгоритму:

· если на графе первого отношения есть дуга, соединяющая пару вершин (x, y), а на графе второго – дуга, соединяющая вершины (y, z), то на графе результирующего отношения изобразить дугу, соединяющую вершины (x, z);

· продолжать до исчерпания всех возможных вариантов.

Конечный результат перемножения не зависит от способа выполнения операции (аналитический или графический).

Через прямое произведение отношений можно определить степени одного отношения:

Q ´ Q = Q ²; Q ´ Q ´ Q = Q ³ и т.д.

Транзитивным замыканием отношения (обозначается Q⁺) называют объединение всех целых степеней отношения Q. Такое определение транзитивного замыкания отношения не дает эффективного алгоритма его построения для заданного отношения (по определению – это бесконечный процесс).

Аналитически это можно записать как объединение степеней множества: Q⁺ = Q È Q² È Q³ È Q ⁴ ..È Qⁿ... или

Q⁺ = È Qⁱ.

(i Î N)

Для практического построения транзитивного замыкания заданного отношения используют следующий алгоритм:

· на графе заданного отношения добавить дуги с использованием свойства транзитивности;

· процесс добавления дуг закончить, если на построенном таким образом графе нельзя уже добавить ни одной дуги (добавленные на предыдущем шаге дуги также участвуют в построении).

Транзитивно–рефлексивное замыкание отношения Q (обозначается Q^* ) – это объединение нулевой степени отношения и транзитивного замыкания отношения: Q^* = Q⁰ È. Q⁺ или

Q^* = È Qⁱ.

(i Î N₀)

Нулевая степень любого отношения, построенного на несущем множестве М = {a,b,c,d}, имеет вид: {aa, bb, cc, dd}.

Граф транзитивно – рефлексивного замыкания отношения легко получить из графа транзитивного замыкания отношения добавлением в каждой вершине дуги – петли, которая связывает вершину саму с собой.

1.9 Упражнения и задачи к главе 1

1 Даны два множества: A = {a, ab, ac} и B = {b, bc, ab}. Найти объединение этих множеств A È B.

2 Дано универсальное множество – множество натуральных чисел W= {1,2,3,...,10} и его подмножества A и B. Найти объединение A È B, если элементы множества A – четные числа, а элементы множества B – нечетные.

3 Даны множества A = {a, b, c}, B = {b, c, d}, C = {d, e, f}. Определить: (A Ç B) и (A Ç B Ç C).

4 Множество В содержит два элемента, а множество А содержит три элемента, такие которые не входят в В, но один элемент множества А входит в множество С. Определить:

(В Ç А), (А Ç В Ç С), (А Ç С). Выбор элементов произвольный.

5 Даны два множества A = {a, c, b, d, e} и B = {a, b, k}. Определить разность: (A \ B) и (B \ A).

6 Даны универсальное множество – множество натуральных чисел W = {1,2,3,...,10} и его подмножество A = {1, 2, 3}. Определить разность (A \ W) и (W \ A).

7 Заданы универсальное множество – множество натуральных чисел W = {1,2,3,...,14}, где n = 14 и его подмножества A = {2, 4, 6, 8} и B = {1, 3, 5, 7}. Найти дополнения A и B.

8 Заданы универсальное множество – множество натуральных чисел W = {1, 2, 3,..., 12} и его подмножество A = {2, 4, 6, 8}.

Найти объединение дополнения A и множества A.

9 Заданы множества B = {a, b, c,..., k}, A = {a} и C = {b, m, z, x, k}. Определить: (B \ A), (A \ B), (B \ A Ç C).

10 Заданы универсальное множество W = {1,2,3,...,20} и его подмножества: A = {i}, B = {3·i} и C = {4·i}, где i =1,2,3... Найти множество (A È B) \ C.

11 Даны два множества A = {a, ab, ac} и B = {b, bc, ab}.

Найти объединение этих множеств A È B и определить количество элементов полученного множества.

12 Даны множество A = {abc, d} и множество B = {ad, a}. Определить: A ´ B (прямое произведение этих множеств).

13 Даны множества C = {d, e, f} и A = {d, f, m}. Определить множества: Z = C È B и D = Z ´ A.

14 Дано множество Y = {a, cb}. Возвести это множество во вторую и в третью степень.

15 Упростить выражения:

а) Ф = А Ç В \ С È В (с помощью диаграмм Венна);

__

б) Ф = (А Ç В) \ (С È В) (с помощью диаграмм Венна);

в) Ф = А Ç В \ С È В (с помощью диаграмм Венна);

_____________

г) Ф = (А \ В) Ç (В \ А) (с помощью диаграмм Венна).

16 Даны бинарные отношения P = {ab, ac, bc} и Q = {cb, ac, bc}. Найти (обратное отношение) и пересечение P^-1 Ç Q.

17 Даны бинарные отношения P = {ab, ac, bc, bd, da} и

Q ={cb, ac, bc, dc}. Определить свойства этих отношений и получить P ´ Q.

18 Для заданного бинарного отношения P = {ab, ac, сc, bd, da} построить P ²,P ³ и P ⁺.

2 Элементы алгебры логики

2.1 Простые высказывания; логические связки

Простые высказывания будем обозначать p, q, r... Основное свойство простого высказывания: высказывание может быть или ложно(False, 0, "Hет") или истинно(True,1, "Да"). В дальнейшем примем обозначения "0" и "1". Для построения составных высказываний будем использовать пять логических связок:

1 Конъюнкция (логическое " И ") – p /\ q.

2 Дизъюнкция (логическое " ИЛИ ") – p \/ q.

3 Отрицание (логическое " Hе ") – ~ p.

4 Эквивалентность (тогда и только тогда) – p º q

5 Импликация (если... то) – p ® q.

p – " жарко ";

q – " идет дождь ";

r – " очень сыро ".

Жарко И идет дождь – p/\q.

Если идет дождь,то очень сыро – p ® q.