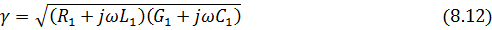
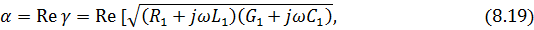
называется коэффициентом ослабления
Мнимая часть комплексного коэффициента передачи линии
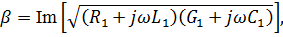
характеризующая изменение фазы прямой и обратной волн на единицу длины линии, называется коэффициентом фазы. Для линии без потерь коэффициент фазы прямо пропорционален частоте:

3) Применение теории цепей с распределенными параметрами при анализе процессов в направляющих системах электросвязи. Коэффициент распространения и волновое сопротивление длинной линии.
Задача анализа цепей с распределенными параметрами обычно сводится к определению законов изменения токов и напряжений вдоль цепи, а также к исследованию частотных или временных характеристик цепи относительно внешних зажимов. С этой целью необходимо найти частные решения дифференциальных уравнений линии (1.44), (1.45) при соответствующих начальных и граничных условиях.
Для решения дифференциальных уравнений линии используют операторный метод, который позволяет перейти от решения дифференциальных уравнений в частных производных для мгновенных значений токов 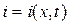 и напряжений
и напряжений 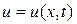 линии к решению обыкновенных дифференциальных уравнений, составленных относительно операторных изображений соответствующих токов
линии к решению обыкновенных дифференциальных уравнений, составленных относительно операторных изображений соответствующих токов 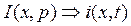 и напряжений
и напряжений 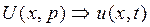 .
.
В курсе ОТЦ показано, что при нулевых начальных условиях, т.е. при 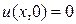 и
и 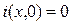 , задача сводится к решению двух дифференциальных уравнений:
, задача сводится к решению двух дифференциальных уравнений:
уравнения, составленного относительно напряжения:

и уравнения, связывающего напряжение и ток:
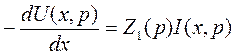
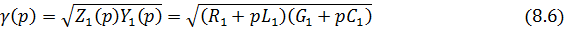
 2015-06-24
2015-06-24 1892
1892