2015-06-24
417
Методы Монте-Карло приближенного вычисления интегралов основаны на использовании равномерно распределенных последовательностей.
Рассмотрим на плоскости некоторую ограниченную область D площадью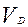 
и предположим, что в ней задана некоторая бесконечная последовательность точек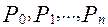 
,….Пусть 
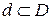некоторая произвольная область площадью 
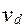. Рассмотрим первые N точек последовательности {Pi} и обозначим через 
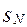число точек из них, попадающих в d. Тогда
Последовательность {Pi} равномерно распределена в D тогда и только тогда, когда
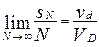
для произвольной области 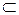d 
D.
Отсюда следует, что при достаточно больших значениях N отношение
,
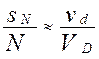откуда площадь области приближенно равна
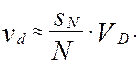(13)
Таким образом, если площадь области D известна, то, генерируя в ней равномерно распределенную последовательность, площадь произвольной области, расположенной в ней, можно определить простым подсчетом числа точек попадающих в последовательность {Pi}.
На этих особенностях и базируется методы приближенного интегрирования Монте-Карло.
Рассмотрим интеграл (1) и для упрощения предположим, что f(x)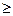 
0. Тогда, значение (1) представляет собой площадь криволинейной фигуры, ограниченной графиком y=f(x), x 
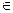[ a, b ]. Возьмем в качестве области D прямоугольник [ a, b; 0, M ], где M 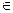max f(x,) площадью 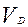= M(b-a) . Далее формируя в D равномерно распределенную последовательность и осуществляя подсчет 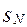,– числа точек попавших в фигуру, ограниченную графиком y=f(x), по формуле (13) определим приближенное значение площади и, тем самым, приближенное значение интеграла(1).
Известны различные способы генерирования равномерно распределенных последовательностей, в частности, случайно распределенные,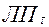 
– последовательности. Более подробно о них см. Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями.–М.: Наука, 1981. -110стр.
