Рассмотрим два из них.
Метод последовательных приближений. Представим в уравнении (1) 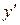 в виде отношения дифференциалов
в виде отношения дифференциалов 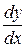 , тогда
, тогда
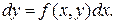
Далее, интегрируя обе части полученного соотношения на промежутке [ x0, x ] получаем
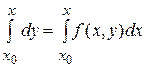 ,
,
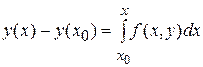
или
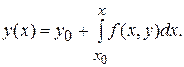 (3)
(3)
Соотношение (3) представляет собой интегральное уравнение, эквивалентное задаче (1), (2). На его основе строится следующий вычислительный процесс
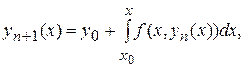 (4)
(4)
где 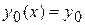 , который и называется методом последовательных приближений. При определенных условиях последовательность функции
, который и называется методом последовательных приближений. При определенных условиях последовательность функции 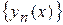 сходится к точному решению задачи (1), (2). А именно,
сходится к точному решению задачи (1), (2). А именно,
Пусть в прямоугольнике 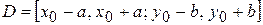 выполнены условия теоремы существования и единственности и
выполнены условия теоремы существования и единственности и 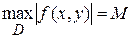 . Тогда в промежутке
. Тогда в промежутке 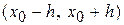 , где
, где 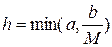 последовательность (4) сходится к точному решению. Причем справедлива следующая оценка
последовательность (4) сходится к точному решению. Причем справедлива следующая оценка

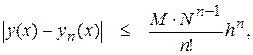
где 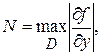
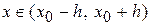 .
.
Для иллюстрации этого метода рассмотрим следующий
Пример. Найти решение задачи Коши
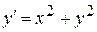 ,
, 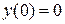 .
.
Найти два первых приближения к решению, оценить погрешность.
Решение. Возьмем в качестве области 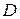 квадрат [-1, 1; -1, 1]. Здесь
квадрат [-1, 1; -1, 1]. Здесь 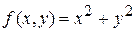 ,
, 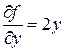 ,
, 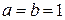 . Тогда
. Тогда
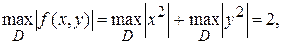
т.е. М=2,
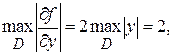
т.е. N=2,
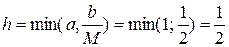 .
.
Погрешность n -го приближения
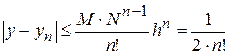 ,
,
отсюда погрешность второго,- 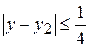 .
.
Найдем приближения 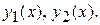 Полагая, что
Полагая, что 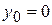 , из (4) имеем
, из (4) имеем
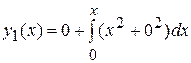 ,
,
т.е. 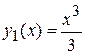 .
.
Тогда
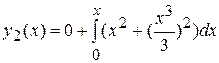
т.е.
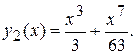
Замечание. В том случае, когда дана погрешность 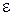 приближенного решения число итераций, т.е. последовательных приближений, можно найти, потребовав
приближенного решения число итераций, т.е. последовательных приближений, можно найти, потребовав
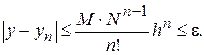
Так, например, в рассмотренном примере
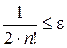 ,
,
откуда 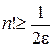 и значение
и значение 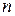 устанавливается последовательным перебором.
устанавливается последовательным перебором.
Метод рядов Тейлора. В этом случае решение задачи (1), (2) ищется в виде ряда
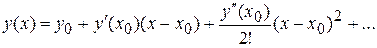 .
.
Значения производных, необходимых для построения решения находятся путем последовательного дифференцирования уравнения (1). Так, непосредственно из него следует
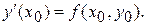
Далее,
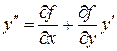 ,
,
тогда
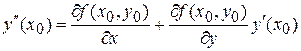
и т.д.
Очевидно, что данная процедура позволяет получить решение со сколь угодно высокой точностью лишь в том случае, когда функция 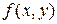 является бесконечно дифференцируемой в точке
является бесконечно дифференцируемой в точке 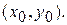 В противном случае данный метод может быть вообще неприменим. См., например, задачу
В противном случае данный метод может быть вообще неприменим. См., например, задачу
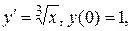
где 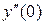 уже не существует.
уже не существует.
 2015-06-24
2015-06-24 508
508








