Стремление повысить точность приближенного вычисления интеграла путем повышения степени интерполяционного многочлена неизбежно приводит к возрастанию технических сложностей при вычислении квадратурных коэффициентов. Поэтому на практике стараются обойтись многочленами невысокой степени, разбивая исходный отрезок интегрирования на меньшие части. В результате этого получают семейства квадратурных правил, зависящих от степени использованных интерполяционных многочленов. Рассмотрим простейшие из них.
Правило прямоугольников. Исходный отрезок [ a,b ] разбивается на n равных частей величиной 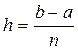 , на каждом из них выбирают по одной точке
, на каждом из них выбирают по одной точке 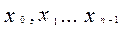 . Далее, применяя к каждой из них формулу (4) получаем правило
. Далее, применяя к каждой из них формулу (4) получаем правило
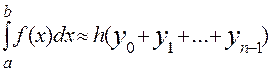 , (8)
, (8)
называемое правилом прямоугольников.
Если f(x) 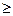 0, то площадь криволинейной трапеции выражаемой
0, то площадь криволинейной трапеции выражаемой 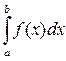 , согласно (8), вычисляется как площадь фигуры, состоящей из прямоугольников с основанием h и высотами
, согласно (8), вычисляется как площадь фигуры, состоящей из прямоугольников с основанием h и высотами 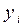 . В зависимости от выбора точек xi различают формулы левых и правых прямоугольников (Рисунок 1).
. В зависимости от выбора точек xi различают формулы левых и правых прямоугольников (Рисунок 1).
а)

б)

Рисунок 1. Правило прямоугольников: а)- левых; б)- правых
Правило трапеций. Разделим отрезок [ a, b ] на n равных частей и обозначим точки деления через 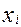 =a+ih,
=a+ih, 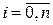 ,
, 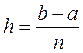 . Применяя, далее, к каждому из отрезков
. Применяя, далее, к каждому из отрезков 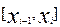 формулу (5), получим квадратурное правило
формулу (5), получим квадратурное правило
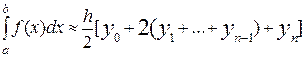 , (9)
, (9)
называемое формулой трапеций. Ее геометрический смысл состоит в замене кривой y=f(x) ломаной и замене криволинейной трапеции, соответствующей участку 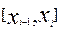 , обычной, – прямолинейной
, обычной, – прямолинейной

Рисунок 2. Правило трапеций
Правило парабол. Разделим отрезок [ a, b ] на n =2m частей, обозначим точки деления через 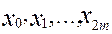 и рассмотрим сдвоенные отрезки. К каждому из них применим формулу (6), в результате чего получим правило
и рассмотрим сдвоенные отрезки. К каждому из них применим формулу (6), в результате чего получим правило
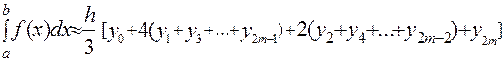 , (10)
, (10)
где 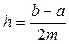 , которое называется формулой парабол или Симпсона. Название также отчасти объясняется геометрическими особенностями, состоящими в том, что на каждом сдвоенном отрезке кривая y=f(x) заменяется участком параболы.
, которое называется формулой парабол или Симпсона. Название также отчасти объясняется геометрическими особенностями, состоящими в том, что на каждом сдвоенном отрезке кривая y=f(x) заменяется участком параболы.
Правило трех восьмых. Разделим исходный отрезок на 3m частей, образуем строенные отрезки 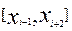 и к каждому из них применим формулу (7). В результате этого получим правило
и к каждому из них применим формулу (7). В результате этого получим правило
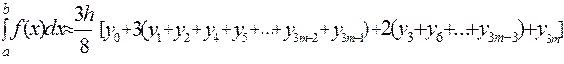 , (11)
, (11)
где 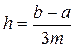 , называемое формулой трех восьмых.
, называемое формулой трех восьмых.
 2015-06-24
2015-06-24 477
477








