2015-06-24
333
Напомним основные положения теории рядов Фурье.
Пусть имеется некоторая функция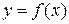 
, заданная на промежутке 
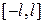и рассматривается бесконечная система функций
.
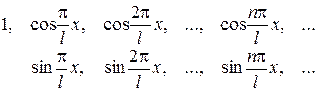Ставится задача о представлении данной функции в виде тригонометрического ряда
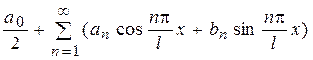(1)
Такое представление при определенных условиях возможно и его коэффициенты вычисляются по следующим формулам
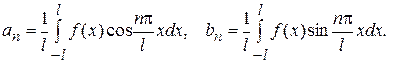(2)
Тригонометрический ряд (1) с коэффициентами (2) называется рядом Фурье функции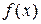 
.
Справедлива следующая теорема о разложимости (т. Дирихле):
Если 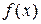кусочно-монотонная функция и имеет не более, чем конечное число точек разрыва первого рода, то ее ряд Фурье (1), (2) сходится к значению 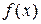в точках ее непрерывности и к среднему арифметическому ее односторонних пределов в точках разрыва.
Так, например, если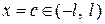 
точка разрыва 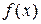, то сумма ряда Фурье в этой точке равна
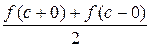- (Рисунок 1),
где
, 
.
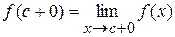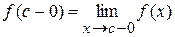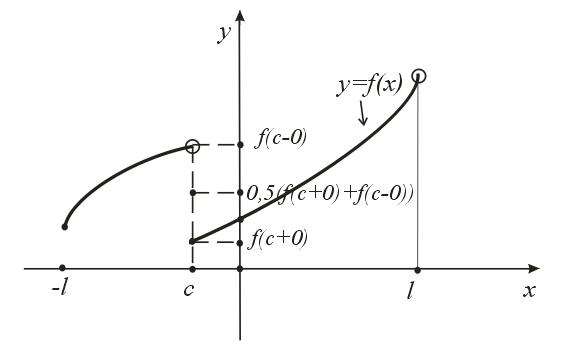
Рисунок 1. Пояснения к теореме Дирихле
Т.о. за исключением, быть может, конечного числа точек сумма ряда Фурье (1), (2) равна .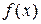
Замечание 1. В точках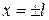 
ряд Фурье сходится к среднему арифметическому правого и левого пределов функции 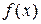в точках 
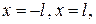соответственно.
Обратим внимание на особенности разложения в ряд Фурье четных и нечетных функций.
Если 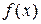четная на отрезке 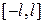, то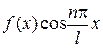 
, также четная, а 
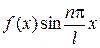, - нечетная. Поэтому коэффициенты
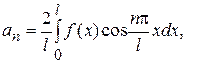
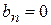
и разложение (1) принимает вид
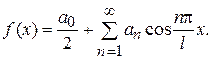
Если же функция 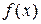нечетная, то 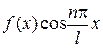также нечетная, а 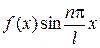, - четная.
Поэтому
, 
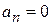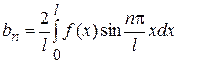
и разложение (1) принимает вид
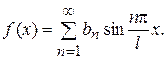
Замечание 2. Выражение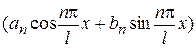 
в разложении (1), вводя вспомогательный угол, можно представить в ви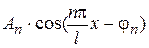де 
, где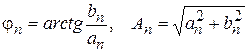 
и ряд в целом
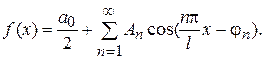
Тогда слагаемые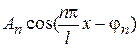 
называются гармоническими составляющими или гармониками, коэффициенты 
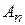- амплитудами гармоник, 
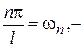частотами, 
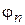- начальными фазами. Иногда гармоника 
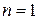называется основной, гармоники 
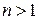, - побочными.
Замечание 3. Иногда тригонометрические разложения заданной функции строятся на промежутке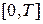 
. В этом случае рассматривается система тригонометрических функций
1,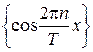 
, 
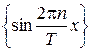
и разложение имеет вид
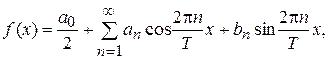(3)
где
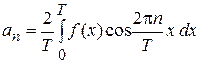(4)
.
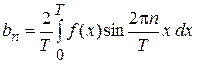Теорема Дирихле для промежутка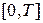 
формулируется соответственно аналогичным образом.
