2015-06-24
10053
Определение 1. 4. 1. Если в группе А даны подмножества М и N, то под произведением М · N этих множеств мы будем понимать множество всех элементов группы А, равных произведению некоторого элемента из М на некоторый элемент из N, т.е. М · N = { а = т · п 
А | т М, n N }, М, N 
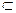А.
Замечание. Множество всех подмножеств группы А – Р (А)относительно введённой операции умножения не является группой. Но если ограничиться только некоторыми подмножествами, в А, то при определённых условиях может получиться группа.
Определение 1. 4. 2. Пусть Н -подгруппа группы А и а А. Тогда произведение аН = { а } · Н = { ah | h Н } называется левым смежным классом (л. с. к.) группы А по подгруппе Н, порождённым элементом а.
Аналогично На = Н · { а } = { ha | h Н } называется правым смежным классом (п. с. к.).
Свойства смежных классов
1) аН = Н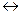 
a Н. В частности, подгруппа Н сама является л.с.к. (п.с.к.) и Н · Н= Н.
2) Эквивалентны условия: а) аН = bН; б )b аН; в) а-1 b Н.
3) Множество всех л.с.к. { аН | а А } образует разбиение группы А.
Поэтому л.с.к., отличные от Н, не являются подгруппами в А.
4) Любые два л.с.к. равномощны друг другу и равномощны Н. Аналогичные свойства верны и для п.с.к..
Доказательство. 1) Пусть аН= Н, тогда а = а · 1 аН = Н.
Пусть а Н. Ясно, что аН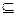 
Н. Если h H, то h = aa-1h aH, т.к. a-1h Н, поэтому Н 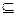аН. Тем самым доказано, что аН = Н.
2)а) => б): b bН = аН.
б)=> в): Если b аН, то b = ah, где h H. Тогда a-1b = h Н.
в)=> а): Пусть a-1b Н. По свойству 1), a-1bН = Н, откуда bН= аН.
3) U аН = А, т.к. любой элемент а А лежит в л.с.к. аН.
Кроме того, два л.с.к. или совпадают, или не пересекаются (т.е. не имеют ни одного общего элемента). Действительно, если аН и bН пересекаются и с аН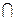 
bH, то в силу 2), аН = сН = bН.
4) Любой класс аН равномощен подгруппе Н: отображение 
: Н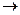 
aН, заданное формулой (h) = ah (
h Н), осуществляет биективное соответствие между ними.
Примеры
1. Найдем все левые и правые смежные классы аддитивной группы < Z, +> целых чисел по подгруппе <3 Z, +> целых чисел, кратных 3. Множества Z и 3 Z можно записать в виде:
Z = {..., - 6, - 5, - 4, -3, -2, - 1, 0, 1, 2, 3, 4, 5, 6,...},
3 Z = {..., -9, - 6, -3, 0, 3, 6, 9, 12,...},
Найдем левые смежные классы для элементов а {0, 1, 2}. Получим
0+ 3 Z = {...,- 9, - 6,- 3, 0,3, 6, 9, 12,...} =3 Z,
1+ 3 Z ={..., - 8, - 5, - 2, 1, 4, 7, 10, 13,...},
2+ 3 Z ={..., - 7, - 4, - 1, 2, 5, 8, 11,...}.
Для элемента а = 4 получим 4 + 3 Z = 1 + 3 Z и т. д. Следовательно, различных левых смежных классов будет всего три: 3 Z, 1 + 3 Z, 2 + 3 Z. Все остальные смежные классы будут совпадать с одним из этих трех классов. Так как < Z, + > - коммутативная группа, то все левые смежные классы будут совпадать с соответствующими правыми классами.
2. Выясним, существуют ли группы и их подгруппы такие, у которых не все левые смежные классы будут совпадать с соответствующими правыми классами. Найдем левостороннее и правостороннее разложения
группы S3 по подгруппе Н = { е,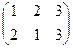 
} и сравним их:
{ е, }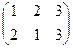 
{ 
, 
} { 
, 
}
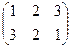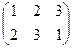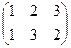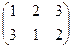{ е, } { , } { , }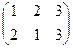
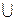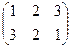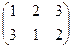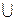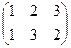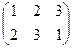Видим, что множество левых смежных классов не совпадает с множеством правых смежных классов.
Теорема 1. 4. 1. (Лагранжа). Порядок любой подгруппы произвольной конечной группы делит порядок самой группы.
Доказательство. Действительно, пусть Н = { h 1 ,..., hn } - подгруппа конечной группы А и в каждом из различных л.с.к. по подгруппе H выбрано по одному элементу a 1 = е, а 2,... ак. По свойству 3), мы получаем левостороннее разложение группы А на попарно непересекающиеся л.с.к.:
А = { h 1,..., hn } 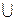{ a 2 h 1 ,…,a 2 hn } 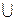... 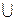{ akh 1..., a k h n },
каждый из которых содержит, по свойству 4), |Н| = п элементов. Итак, А является объединением к непересекающихся п - элементных подмножеств. Следовательно, |А| = п ∙ к и порядок Н делит порядок А.
Определение 1. 4. 3. Число к различных л.с.к. группы А по подгруппе Н называется индексом подгруппы Н в группе А и обозначается (А: Н).
Замечания. 1) Поскольку индекс единичной подгруппы {1} в группе А равен порядку А, то теорему Лагранжа можно сформулировать так:
(А : {1}) = (A: Н) ∙ (Н: {1}).
2) Все полученные результаты справедливы и для п.с.к..
Теорема 1. 4. 2. Для того, чтобы множество всех л.с.к. группы А по подгруппе Н было группой относительно умножения подмножеств, необходимо и достаточно, чтобы оно было замкнуто относительно этой операции.
Доказательство.
Необходимость очевидна.
Достаточность. Пусть множество { аН| а А} замкнуто относительно умножения. Тогда (аН) ∙ (bН) = (аb) Н, т.к. (аН) ∙ (bН) - л.с.к., содержащий аb. Ясно, что Н - единица и (аН) ∙ (а -1 Н) - Н, т.е. а -1 Н - обратный к аН.
