Критерий разложения группы в прямое произведение двух групп
Пусть даны две абстрактные группы < А, ∙> и < В, *>. Построим с помощью этих групп новую группу. Для этого нам нужно указать элементы новой группы и групповую операцию. Пусть элементами новой группы будут пары элементов (а, b), где a  А, b
А, b  В, то есть множеством - носителем новой группы будет декартово произведение
В, то есть множеством - носителем новой группы будет декартово произведение
А × В= {(а, b) | а  А, b
А, b  В }.
В }.
Операцию на множестве А × В определим так:
 (а, b),(с, d)
(а, b),(с, d)  А × В (a, b)
А × В (a, b)  (c, d) = (a ∙ с, b * d),
(c, d) = (a ∙ с, b * d),
то есть над первыми компонентами пары производится операция, заданная в группе < А, ∙ >, а над вторыми - операция, заданная в группе < В, *>.
Теорема 2. 2. 1. < А × В,  > - группа.
> - группа.
Доказательство. Очевидно, что определенная нами операция  является бинарной алгебраической на А × В. Проверим выполнение аксиом группы на множестве А × В.
является бинарной алгебраической на А × В. Проверим выполнение аксиом группы на множестве А × В.
1) (ассоциативность)  (а, b), (с, d), (t, f)
(а, b), (с, d), (t, f)  A × В ((а, b)
A × В ((а, b)  (с, d))
(с, d))  (t, f) = = (а ∙ с, b * d)
(t, f) = = (а ∙ с, b * d)  (t, f) = ((а ∙ с)∙ t, (b* d) *f) = (а ∙(с ∙ t), b * (d *f)) = (a, b)
(t, f) = ((а ∙ с)∙ t, (b* d) *f) = (а ∙(с ∙ t), b * (d *f)) = (a, b) 
 (с ∙ t) ,d*f) = (а, b)
(с ∙ t) ,d*f) = (а, b)  ((с, d)
((с, d)  (t, f)).
(t, f)).
2) (наличие нейтрального элемента) (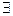 (еА, еB)
(еА, еB)  А × В)(
А × В)( (a, b)
(a, b)  А × В)(е А, ен)
А × В)(е А, ен)  (а, b) = (а, b)
(а, b) = (а, b)  (е A, еB) = (а, b).
(е A, еB) = (а, b).
3) (наличие симметричного элемента)  (а, b)
(а, b)  А × В
А × В 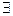 (а ', b ')
(а ', b ')  А × В (а, b)
А × В (а, b)  (а ', b ') = (а ', b ')
(а ', b ') = (а ', b ')  (а, b) = (еА, еB). Здесь а' - элемент симметричный к а в группе А; b ' - элемент симметричный к b в группе В.
(а, b) = (еА, еB). Здесь а' - элемент симметричный к а в группе А; b ' - элемент симметричный к b в группе В.
Из выше сказанного следует, что < А × В,  > является группой по определению.
> является группой по определению.
Определение 2. 2. 1. Группа G = < А × В,  > называется внешним прямым произведением групп < А, ∙ > и < В, *> и обозначается G = А
> называется внешним прямым произведением групп < А, ∙ > и < В, *> и обозначается G = А  В.
В.
Замечание. Если группы < А, ∙ > и < В, *> - аддитивные, то говорят о прямой сумме, то есть G =А 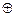 В.
В.
Пример 1. Найдем прямую сумму двух групп < R, +> и < R, +>.
R 2 = R × R = {(a, b) | а  R, b
R, b  R } = R
R } = R 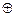 R
R
(а, b) 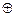 (с, d) = (а + с, b + d), то есть R 2 - аддитивная группа двумерных арифметических векторов.
(с, d) = (а + с, b + d), то есть R 2 - аддитивная группа двумерных арифметических векторов.
2. Поле комплексных чисел является прямой суммой двух абелевых групп А = < R, +> и В = < Ri,+>; С = R 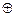 Ri; (a, bi)
Ri; (a, bi) 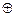 (с, di) = (а + с, (b + d) i).
(с, di) = (а + с, (b + d) i).
Замечание. Вгруппе G = А  В можно выделить две подгруппы:
В можно выделить две подгруппы:
G1 = < A × { еB }, ∙ >, где A ×{ eB } = {(a, eB)| a  A, е B
A, е B  В } и G2 = <{ еA } × В, ∙ >, где { еA } × В = {(еA, b) | еА
В } и G2 = <{ еA } × В, ∙ >, где { еA } × В = {(еA, b) | еА  А, b
А, b  В }. Зададим отображения:
В }. Зададим отображения:
 : А
: А 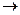 G 1
G 1  :а
:а 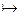 (а, е B) и
(а, е B) и 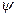 :В
:В 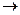 G 2,:
G 2,: 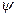 : b
: b 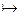 (е A, b).
(е A, b).
Легко проверить, что отображение  является изоморфным отображением группы А на G 1, а отображение
является изоморфным отображением группы А на G 1, а отображение 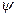 - изоморфизмом группы В на G 2.
- изоморфизмом группы В на G 2.
Следовательно, группа G = А 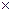 В будет содержать подгруппы G 1; и G 2, изоморфные А и В, т.е. A
В будет содержать подгруппы G 1; и G 2, изоморфные А и В, т.е. A 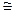 G 1, В
G 1, В 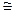 G 2.
G 2.
Теорема 2. 2. 2. В группе G= А 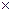 В подгруппы G 1 и G 2 являются нормальными делителями, причем G 1
В подгруппы G 1 и G 2 являются нормальными делителями, причем G 1 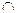 G 2 = { еG }.
G 2 = { еG }.
Доказательство. 1. Покажем, что подгруппы G 1 и G 2 замкнуты относительно взятия сопряженных элементов.
 (a, eB)
(a, eB)  G 1
G 1  (c, d)
(c, d)  G (с, d)(a, еB)(с, d)-1 = (са, d)(c -1, d -1)= (сас -1, ев)
G (с, d)(a, еB)(с, d)-1 = (са, d)(c -1, d -1)= (сас -1, ев)  G 1
G 1 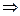
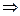 G 1
G 1 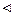 G.
G.
Аналогично:
 (eA,b)
(eA,b)  G 2
G 2  (c, d)
(c, d)  G (с, d)(eA,b)(с, d)-1 = (с, db)(c -1, d -1)=(eA,dbd -1)
G (с, d)(eA,b)(с, d)-1 = (с, db)(c -1, d -1)=(eA,dbd -1)  G 2
G 2 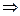 G 2
G 2 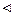 G.
G.
2. Очевидно, что G 1 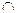 G2=(eA,eB)
G2=(eA,eB)  G, действительно, если с
G, действительно, если с  G 1
G 1 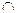 G 2
G 2 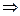 с
с  G 1и с
G 1и с  G 2
G 2 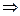 [ с = (а, еB)] и [с = (eA, b)]
[ с = (а, еB)] и [с = (eA, b)] 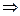 (а = eA) и (b = еB)
(а = eA) и (b = еB) 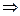 c = (e A, еB)= еG
c = (e A, еB)= еG  G.
G.
Теорема 2. 2. 3. Любой элемент группы G= А 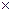 В однозначно представим в виде произведения g = g 1 ∙ g2, где g 1
В однозначно представим в виде произведения g = g 1 ∙ g2, где g 1  G 1, g2
G 1, g2  G 2, g
G 2, g  G.
G.
Доказательство. Действительно, любой элемент g может быть представлен в виде: g = (a, b) = (а, еB) ∙(еА, b), где (а, еB)  G 1, (eA, b)
G 1, (eA, b)  G2.
G2.
Если g = (a, b) = (a', eB)(eA,b') = (a', b'), то а = a' и b = b'.
Итак, группа G порождается подгруппами G 1 и G 2, то есть G = G 1 ∙ G 2.
Замечание. Рассмотренная выше конструкция (G = А 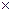 В) внешнего прямого произведения групп позволяет из двух заданных групп построить новую, более сложно устроенную группу, причем, если |А| = п, |В| = k, то | G | = пk. Понятно, что в общем случае можно рассматривать и группу
В) внешнего прямого произведения групп позволяет из двух заданных групп построить новую, более сложно устроенную группу, причем, если |А| = п, |В| = k, то | G | = пk. Понятно, что в общем случае можно рассматривать и группу
G = А 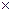 А2
А2 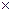 ...
... 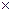 Ак.
Ак.
Но если нам дана сложно устроенная группа G, то для того что бы ее разложить в прямое произведение двух других групп нам потребуется следующая теорема.
Теорема 2. 2. 4. Для того, чтобы группа G была изоморфна прямому произведению двух групп А и В, необходимо и достаточно, чтобы группа G содержала нормальные делители G 1и G 2, изоморфные, соответственно группам А и В, чтобы пересечение G 1 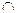 G 2 = { еG } и чтобы группа G порождалась нормальными делителями G 1, и G2.
G 2 = { еG } и чтобы группа G порождалась нормальными делителями G 1, и G2.
Доказательство. Нужно доказать, что G 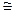 А
А 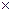 B
B 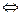 (C 1
(C 1 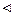 G) и (G 2
G) и (G 2 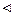 G) и (G 1
G) и (G 1 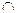 G 2 ={ еG }) и (G 1
G 2 ={ еG }) и (G 1 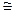 A) и(C 2
A) и(C 2 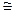 B) и (G = G 1 ∙ G 2).
B) и (G = G 1 ∙ G 2).
Необходимость указанных условий следует из теорем 2.2.2 и 2.2.3, докажем достаточность, то есть если (C 1 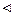 G) и (C 2
G) и (C 2 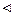 G) и (G 1
G) и (G 1 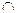 G 2 ={ еG }) и (G 1
G 2 ={ еG }) и (G 1 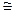 A) и (C 2
A) и (C 2 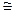 B) и (G = G 1 ∙ G 2), то Gбудет изоморфна А
B) и (G = G 1 ∙ G 2), то Gбудет изоморфна А 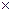 B.
B.
Сначала докажем, что если две нормальных подгруппы G 1 и G 2 группы G пересекаются по { еG } то они поэлементно перестановочны, то есть  (h 1
(h 1  G 1)
G 1)  (h 2
(h 2  G 2)[ h 1 ∙ h2 = h2 ∙ h 1] Действительно, рассмотрим элемент
G 2)[ h 1 ∙ h2 = h2 ∙ h 1] Действительно, рассмотрим элемент
c = h 1 ∙ h2 ∙ h 1-1∙ h2 -1. Если в этой записи скобки расставить так: c = (h 1∙ h2 ∙ h 1-1)∙ h2,то видно, что элемент с принадлежит группе G2 (G 2 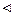 G).
G).
Аналогично, записав элемент с в виде: c = h 1 ∙ (h2 ∙ h 1-1∙ h2 -1), видим, что с  G1 (G 1
G1 (G 1 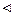 G). Таким образом,
G). Таким образом,  G 1
G 1 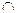 G 2, а так как G 1
G 2, а так как G 1 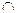 G 2={ e G}, то c = h 1 ∙(h2 ∙ h 1-1∙ h2 -1)= еG
G 2={ e G}, то c = h 1 ∙(h2 ∙ h 1-1∙ h2 -1)= еG 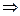 h 1 ∙ h2 = h 2 ∙ h 1. По условию теоремы дано, что группа G порождается своими нормальными делителями G 1 и G 2, это означает, с учетом доказанной перестановочности G 1 и G 2, что каждый g
h 1 ∙ h2 = h 2 ∙ h 1. По условию теоремы дано, что группа G порождается своими нормальными делителями G 1 и G 2, это означает, с учетом доказанной перестановочности G 1 и G 2, что каждый g  G представим в виде произведения g = g 1 ∙ g2, где g 1
G представим в виде произведения g = g 1 ∙ g2, где g 1  G 1, g2
G 1, g2  G 2, то есть G = G 1 ∙ G 2. Покажем, что это представление однозначно. Предположим противное. Пусть g = g 1 ∙ g2, и g = с 1 ∙ с2, где g 1 c 1
G 2, то есть G = G 1 ∙ G 2. Покажем, что это представление однозначно. Предположим противное. Пусть g = g 1 ∙ g2, и g = с 1 ∙ с2, где g 1 c 1  G 1, g 2, c 2
G 1, g 2, c 2  G 2, тогда
G 2, тогда
g 1∙ g2=с 1∙ с2 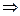 c 1-1∙ g 1 =c 2∙ g 2-1
c 1-1∙ g 1 =c 2∙ g 2-1  G 1
G 1 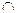 G 2
G 2 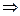 c 1-1∙ g 1= c 2∙ g 1-= eG
c 1-1∙ g 1= c 2∙ g 1-= eG 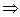
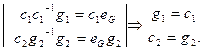
Зададим теперь отображение  : G
: G 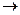 A
A 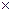 B которое любому элементу g
B которое любому элементу g  G равному g = g 1 ∙ g 2, где g 1
G равному g = g 1 ∙ g 2, где g 1  G 1, g 2
G 1, g 2  G 2 ставит в соответствие пару (g 1, g2)
G 2 ставит в соответствие пару (g 1, g2)  A x В, то есть
A x В, то есть  : g
: g 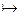 (g 1, g2). Это отображение будет изоморфизмом.
(g 1, g2). Это отображение будет изоморфизмом.
Действительно: а) сюръективность отображения  очевидна, так как
очевидна, так как
 (g 1, g2)
(g 1, g2)  A
A 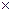 B
B 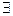 (g = g 1 ∙ g2)
(g = g 1 ∙ g2)  G:
G:  (g)= (g 1∙ g2).
(g)= (g 1∙ g2).
б) докажем инъективность отображения  :
:  a, b
a, b  G,(a = a l a2)и(b = b 1 b 2),если
G,(a = a l a2)и(b = b 1 b 2),если  (а)=
(а)=  (b),то(а 1, а 2)=(b 1, b 2)
(b),то(а 1, а 2)=(b 1, b 2) 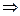 (а 1= b 1 ) и (а 2 = b 2)
(а 1= b 1 ) и (а 2 = b 2) 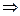 (а = b).
(а = b).
Проверим, что отображение  гомоморфно. В силу поэлементной перестановочности групп G 1 и G 2 имеем:
гомоморфно. В силу поэлементной перестановочности групп G 1 и G 2 имеем:
 a, b
a, b  G, a ∙ b = (a 1 ∙ a 2) ∙ (b 1 ∙ b 2) = (a 1 ∙ b 1) ∙ (а 2 ∙ b 2).
G, a ∙ b = (a 1 ∙ a 2) ∙ (b 1 ∙ b 2) = (a 1 ∙ b 1) ∙ (а 2 ∙ b 2).
Итак, мы разложили группу G в прямое произведение своих нормальных подгрупп G 1 и G 2. При этом, каждый элемент группы G однозначно представим в виде произведения g 1 ∙ g2, где g 1  G 1, g 2
G 1, g 2  G 2, а операция умножения определяется по правилу: а ∙ b = (a 1 ∙ b 1) ∙ (а 2 ∙ b 2).
G 2, а операция умножения определяется по правилу: а ∙ b = (a 1 ∙ b 1) ∙ (а 2 ∙ b 2).
В этом случае говорят о внутреннем прямом произведении нормальных подгрупп G 1 и G 2 группы G.
Замечание. Отличие внутреннего произведения от внешнего прямого произведения состоит в том, что G содержит в качестве прямых множителей сами группы, а не их изоморфные образы.
Разумеется, внешнее прямое произведение А = А 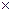 В является также внутренним произведением подгрупп А
В является также внутренним произведением подгрупп А 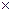 { еB },{ еA }
{ еB },{ еA } 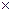 В, и при некотором навыке можно не делать различия между ними, употребляя сокращенное словосочетание «прямое произведение».
В, и при некотором навыке можно не делать различия между ними, употребляя сокращенное словосочетание «прямое произведение».
Проиллюстрируем на примере последнюю теорему
Пример. Группа Клейна разлагается во внутреннее прямое произведение двух циклических подгрупп второго порядка:
Н 4 = { 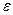 , (1, 2)(3, 4), (1, 3)(2, 4), (1,4)(2, 3)} = ((1, 2)(3, 4))
, (1, 2)(3, 4), (1, 3)(2, 4), (1,4)(2, 3)} = ((1, 2)(3, 4))  ((1, 3)(2, 4)).
((1, 3)(2, 4)).
Действительно, обозначим, G 1 = { 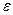 , (12)(34)}, G 2 = {
, (12)(34)}, G 2 = { 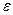 , (13)(24)}.
, (13)(24)}.
1. Подгруппы G 1 и G 2 являются нормальными подгруппами группы Н 4.
(Н 4: G 1) = 2, (Н 4: G 2) = 2. А известно, что подгруппы индекса 2 являются нормальными т.е., G 1 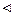 H 4 и G 2
H 4 и G 2 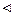 Н 4.
Н 4.
2. Пересечение данных подгрупп состоит только из тождественной подстановки G 1 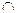 G 2 = {
G 2 = { 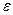 ,(1, 2)(3, 4)}
,(1, 2)(3, 4)} 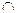 {
{ 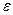 , (1, 3)(2,4)} = {
, (1, 3)(2,4)} = { 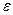 }
}
3. Группа Н4 порождается подгруппами G 1и G 2, подстановки (1, 2)(3, 4) и (1, 3)(2,4) является образующими элементами группы Н 4:
((1,2)(3,4))1=(1,2)(3,4),
((1, 2)(3, 4))2= (1, 2)(3, 4)(1, 2)(3, 4) = (1)(2)(З)(4)= 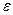
((1, 3)(2, 4))1 = (1, 3)(2, 4), ((1, 3)(2, 4)) 2 = (1, 3)(2,4)(1, 3)(2, 4) = 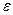
(1,2)(3, 4)(1, 3)(2,4) = (1, 3)(2, 4)(1, 2)(3, 4) = (1,4)(2, 3), ((1, 4)(2, З))2 = 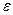
Получаем Н 4 = { 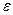 , (1, 2)(3, 4), (1, 3)(2, 4), (1, 4)(2, 3)}.
, (1, 2)(3, 4), (1, 3)(2, 4), (1, 4)(2, 3)}.
Таким образом, группа Н 4 порождается подгруппами G 1и G 2, т.е.
Н 4 = ((1, 2)(3, 4)) ∙ ((1, 3) ∙ (2, 4)) = G 1∙ С 2
Все требования теоремы 2.2.4 выполняются, следовательно, группа Клейна разлагается в прямое произведение двух своих подгрупп второго порядка (Н 4 = G 1  G 2).
G 2).
Замечание. Для всякой группы G существует тривиальное разложение в прямое произведение нормальных делителей { eG } и G.
Рассмотренный ранее пример показывает, что прямое произведение двух конечных циклических групп не обязательно является циклической группой. В следующей теореме формулируются необходимые и достаточные условия, при выполнении которых когда прямое произведение двух конечных циклических групп само является циклической группой.
Теорема 2. 2. 5. Для того, чтобы прямое произведение двух конечных циклических групп порядков т и п было циклической группой, необходимо и достаточно, чтобы числа т и п были взаимно простыми.
Доказательство. Пусть даны циклические группы (а) и (b) порядков т и п соответственно. Докажем сначала необходимость. Предположим, что (а) 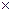 (b) - циклическая группа с образующим (аs, bt). Тогда (аs, bt) i = (а, еB) и (аs, bt)j = (еА, b) для некоторых целых чисел i, j. Имеем равенства: аsi = а, bti= еB, аsj = еA, btj = b. Откуда по пункту 2) из теоремы о свойствах мультипликативной группы, числа si - 1 и sj кратны т, а числа ti и tj - 1 кратны п. Если бы числа т, п не были взаимно простыми, то у них нашелся бы общий простой делитель р. Но тогда числа si - 1 и sj и tj - 1 также делятся на р, и последовательно получаем: s не делится на р, j кратно р и 1 делится на р, что невозможно. Следовательно, НОД(т, п) =1.
(b) - циклическая группа с образующим (аs, bt). Тогда (аs, bt) i = (а, еB) и (аs, bt)j = (еА, b) для некоторых целых чисел i, j. Имеем равенства: аsi = а, bti= еB, аsj = еA, btj = b. Откуда по пункту 2) из теоремы о свойствах мультипликативной группы, числа si - 1 и sj кратны т, а числа ti и tj - 1 кратны п. Если бы числа т, п не были взаимно простыми, то у них нашелся бы общий простой делитель р. Но тогда числа si - 1 и sj и tj - 1 также делятся на р, и последовательно получаем: s не делится на р, j кратно р и 1 делится на р, что невозможно. Следовательно, НОД(т, п) =1.
Достаточность. Пусть т и п - взаимно простые числа. Тогда mu+ nv = 1 для некоторых целых чисел u, v. Покажем, что элемент (а, b)является образующим группы (а) 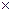 (b).
(b).
Так как (ax, by) = (а, еB) x ∙ (еА, b) y при любых целых х и у, то достаточно убедиться, что элементы (а, еB) и (еА, b) являются целыми степенями (а, b). Учитывая равенство mu + nv = 1, получаем:
(а, b) nv = (а1-mu, bnv ) = (а, еB) и (а, b) ти = (аmu, b1-nv) = (еА, b).
Замечание. Теорема 2.2.5 имеет следующую аддитивную форму:
Zm 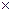 Zn
Zn 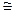 Zmn
Zmn 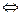 НОД (m, n) = 1.
НОД (m, n) = 1.
Теорема 2. 2. 6. Существует ровно d = НОД (m, n) гомморфизмов циклической группы m -го порядка в циклическую группу n -го порядка. Каждый такой гомоморфизм определяется переводом зафиксированного образующего первой группы в один из элементов подгруппы порядка d второй группы.
 2015-06-24
2015-06-24 6919
6919








