Группы чисел, рассматриваемых по модулю
Рассмотрим аддитивные и мультипликативные группы из теории чисел по модулю m.
Определение 2. 3. 1. Целые числа а и b называются сравнимыми по модулю т, если при делении на т они дают одинаковые остатки.
Обозначение: а  b (mod т).
b (mod т).
Замечания 1. Данное определение эквивалентно следующим: «Целые числа а и b называются сравнимыми по модулю т, если (а - b) 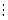 т»; «Целые числа а и b называются сравнимыми по модулю т, если (
т»; «Целые числа а и b называются сравнимыми по модулю т, если (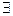 k
k  Z) а-b= п · к».
Z) а-b= п · к».
2. Легко доказать следующие свойства сравнений:
1) (рефлексивность)( a
a  Z) a
Z) a  а (mod т);
а (mod т);
2) (симметричность) ( а, b
а, b  Z) a
Z) a  b (mod т)
b (mod т) 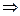 b
b  a (mod m);
a (mod m);
3) (транзитивность)( a, b, c
a, b, c  Z) a
Z) a  b (mod m) и b
b (mod m) и b  c (mod m)
c (mod m) 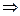 a
a  c (mod m).
c (mod m).
Таким образом, отношение «сравнимости по модулю т» является отношением эквивалентности и разбивает множество всех целых чисел на классы эквивалентности, называемые классами вычетов по модулю т.
Определение 2. 3. 2. Множество целых чисел, которые при делении на число т дают одинаковые остатки, называется классом вычетов по модулю т.
Обозначение: Zm = { 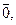
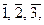
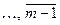 } - множество классов вычетов по модулю т.
} - множество классов вычетов по модулю т.
Пример. Z 5 = { 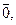
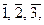
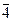 } - множество классов вычетов по модулю 5.
} - множество классов вычетов по модулю 5.
Определение 2. 3. 3. Суммой (произведением) классов вычетов  и
и  по модулю т называется класс вычетов
по модулю т называется класс вычетов 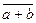 (
(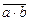 ) по модулю т, то есть класс чисел, содержащий число а + b (а ∙ b).
) по модулю т, то есть класс чисел, содержащий число а + b (а ∙ b).
Пример. Пусть Z 6 = { 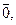
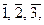
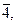
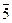 } - множество классов вычетов по модулю 6.
} - множество классов вычетов по модулю 6.
1. Вычислим сумму: 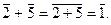
2. Вычислим произведение: 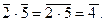
Поскольку каждый класс вычетов по модулю т содержит бесконечное множество чисел, то при сложении (умножении) классов вычетов  и
и  по модулю т, числа а и b можно заменять любыми числами а 1 и b 1,принадлежащими этим же классам вычетов по модулю т.
по модулю т, числа а и b можно заменять любыми числами а 1 и b 1,принадлежащими этим же классам вычетов по модулю т.
Теорема 2. 3. 1. Сумма (произведение) классов вычетов по модулю т определяется однозначно и не зависит от выбора отдельных представителей классов вычетов по модулю т, используемых при составлении суммы (произведения).
Доказательство. 1. Пусть а 1 
 , b 1
, b 1 
 , то а
, то а  a (mod т), b 1
a (mod т), b 1  b (mod т). Сравнения по одному и тому же модулю можно почленно складывать, поэтому а 1 + b 1
b (mod т). Сравнения по одному и тому же модулю можно почленно складывать, поэтому а 1 + b 1  a + b (mod т). Поскольку
a + b (mod т). Поскольку  =
= 
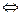 a
a  b (mod т), получаем
b (mod т), получаем 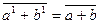 , следовательно,
, следовательно, 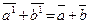 . Таким образом, сумма классов вычетов по модулю т не меняется от замены а и b числами а 1 и b 1.
. Таким образом, сумма классов вычетов по модулю т не меняется от замены а и b числами а 1 и b 1.
Сумма классов вычетов  и
и  по модулю т содержит сумму любых чисел а 1 и b 1, таких что а 1
по модулю т содержит сумму любых чисел а 1 и b 1, таких что а 1 
 , b 1
, b 1 
 .
.
И наоборот, любое с 
 +
+  можно представить в виде с = а 1+ b 1, где а 1
можно представить в виде с = а 1+ b 1, где а 1 
 , b 1
, b 1 
 .
.
Действительно, с 
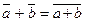 означает, что с
означает, что с  а + b (modт), тогда с - а
а + b (modт), тогда с - а  b (mod т), с-а
b (mod т), с-а 
 , то есть с можно представить в виде с = а 1 + b 1, где а 1 =а
, то есть с можно представить в виде с = а 1 + b 1, где а 1 =а  а, b 1 = с - а
а, b 1 = с - а  b.
b.
2. Аналогично теорема доказывается для произведения классов вычетов.
Теорема 2. 3. 2. < Zm, +> - группа.
Доказательство. Учитывая результат теоремы 2.3.1, заметим, что операция сложения определена корректно и является бинарной алгебраической на множестве Zm. Остается проверить выполнимость аксиом аддитивной группы.
1) ассоциативность операции сложения в Zm выводится из ассоциативности сложения целых чисел:
(
 ,
,  ,
, 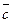
 Zm)
Zm) 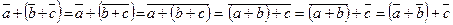 .
.
2) (существование нулевого элемента)
Роль нулевого элемента выполняет класс 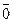
 Zm. Действительно:
Zm. Действительно:
(

 Zm)
Zm)  +
+ 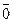 =
= 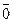 +
+  =
=  .
.
3) (существование для каждого элемента противоположного ему)
Для класса 
 Zm противоположным классом является класс
Zm противоположным классом является класс 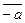
 Zm, то есть класс, содержащий число (- а). Действительно,
Zm, то есть класс, содержащий число (- а). Действительно, 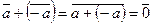 .
.
Таким образом, < Zm, + > - группа. Теорема доказана.
Пример. < Z 6 = { 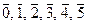 }, +> -группа.
}, +> -группа.
Замечание. Легко доказать, что < Zn, +, ∙ > - коммутативное кольцо. Оно называется кольцом классов вычетов по модулю т.
Обозначим Zp * = Zp \ {0} - множество ненулевых классов вычетов по простому модулю р.
Теорема 2. 3. 3. Пусть р - простое число. < Zp *, •> - группа.
Доказательство. Рассмотрим Zp * ={ 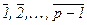 }множество
}множество
ненулевых классов вычетов по простому модулю р с операцией умножения
(
 ,
, 
 Zp *)
Zp *) 
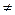
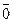 ,
, 
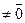
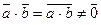
Учитывая результат теоремы 2.3.1. заметим, что данная операция определена корректно и является бинарной алгебраической на множестве Zp *. Остается проверить выполнимость аксиом мультипликативной группы.
1) ассоциативность операции умножения в Zp * выводится из ассоциативности умножения целых чисел:
(
 ,
,  ,
, 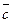
 Zp *)
Zp *) 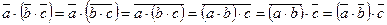 .
.
2) (существование единицы). Очевидно, что роль единицы выполняет класс 
 Zp *. Действительно, (
Zp *. Действительно, (

 Zp *)
Zp *) 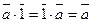 .
.
3) (существование для каждого элемента ему обратного). Пусть 
 Zp *. Очевидно, что 1
Zp *. Очевидно, что 1 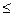 а
а 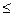 р, поэтому (а, р) = 1. Отсюда по теореме о линейном разложении НОД найдутся x, y
р, поэтому (а, р) = 1. Отсюда по теореме о линейном разложении НОД найдутся x, y  Zp * такие, что ах + рх = 1. Тогда
Zp * такие, что ах + рх = 1. Тогда 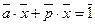 или
или 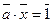 , так как
, так как 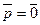 , т.е.
, т.е. 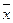
 Zp * есть вычет обратный к
Zp * есть вычет обратный к  .
.
Примеры: 1. Z 3* = { 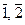 }. Умножение в Z 3* зададим таблицей Кэли:
}. Умножение в Z 3* зададим таблицей Кэли:
| · |  |  |
 |  |  |
 |  |  |
Из таблицы ясно, что: ( )-1 =
)-1 =  , (
, ( )-1 =
)-1 =  .
.
2. Z 5 * = { 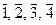 } Умножение в Z 5 * зададим таблицей Кэли:
} Умножение в Z 5 * зададим таблицей Кэли:
 |  |  | 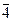 | |
 |  |  |  | 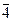 |
 |  | 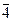 |  |  |
 |  |  | 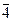 |  |
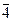 | 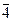 |  |  |  |
Доказательство некоторых теорем теории чисел
теоретико-групповыми методами
Теорема 2. 3. 4. Если 
 Zp, то
Zp, то 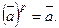
Доказательство. По теореме 2. 3. 3 < Z p *, ·> — группа, | Z p *| = р- 1. Согласно следствия из теоремы Лагранжа, имеем: (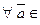 Z p *) | Z p *|
Z p *) | Z p *| 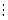 |
|  |. Обозначим |
|. Обозначим |  | = т. Получим (р-1)
| = т. Получим (р-1) 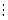 m, т.е.
m, т.е. 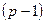 = m · d, d
= m · d, d  N. Но (
N. Но ( ) m =
) m =  , поэтому
, поэтому 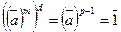 . Домножим обе части равенства
. Домножим обе части равенства 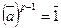 на
на  , получим
, получим 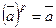 . Последнее равенство верно и для класса
. Последнее равенство верно и для класса  =
= 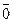 . Итак, (
. Итак, (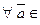 Z p)
Z p) 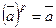 .
.
Следствие 2. 3. 5. (Теорема Ферма). Пусть р - простое число, а  N, тогда ар
N, тогда ар  a ( mod т).
a ( mod т).
Доказательство непосредственно следует из предыдущей теоремы, так как 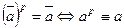 ( mod т).
( mod т).
Теперь рассмотрим множество классов вычетов по модулю т, где число т не обязательно простое.
Лемма 2. 3. 6. Числа а и от взаимно просты тогда и только тогда, когда класс вычетов  по mod т обратим в Zm (т.е. (а, т) = 1
по mod т обратим в Zm (т.е. (а, т) = 1 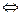 (
(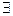

 Zm)
Zm)  ·
·  =
=  .
.
Доказательство. 1. Если а и т взаимно просты, то ab + mc = 1 для некоторых целых чисел b, с (по теореме о линейном разложении НОД). Переходя к классам вычетов по модулю т, получаем
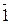 =
=  ·
·  +
+ 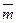 ·
· 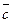 =
=  ·
·  +
+ 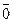 ·
· 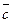 =
=  ·
·  .
.
2. Если  ·
·  =
= 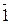 , то a · b
, то a · b  l (mod m), откуда и следует взаимная простота чисел а и т.
l (mod m), откуда и следует взаимная простота чисел а и т.
Примеры: 1. Среди классов вычетов по модулю 12 обратимы в Z 12 классы вычетов, соответствующие натуральным числам меньшим 12 и взаимно простым с 12: { 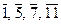 }, здесь
}, здесь 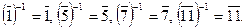
2. Вычислим 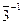 в Z 5. НОД (3, 5) = 1, так что класс
в Z 5. НОД (3, 5) = 1, так что класс 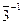 существует.
существует.
Чтобы его найти, представим 1 в виде:
1= 3 b + 5 c, где a, b  Z. (1)
Z. (1)
Переходя к классам вычетов по модулю 5, получим:
 =
= 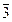 ·
·  +
+ 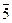 ·
· 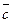 =
= 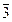 ·
·  +
+ 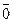 ·
· 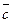 =
= 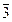 ·
·  ,
,  =
= 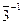 .
.
Представление (1) можно найти с помощью алгоритма Евклида для чисел 5 и 3. Итак, 5= 3 · 1 + 2, 3= 2 · 1 + 1, 2= 2 · 1. НОД (5, 3)= 1= 3 - 2 · 1; 2= 5-3· 1, поэтому 1 = 3 - 2 · 1= 3 - (5 - 3) = 3 · 2 + 5 · (-1);  =
= 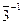 =
=  .
.
Теорема 2. 3. 7. Пусть Zm * - множество классов вычетов по модулю т, соответствующих натуральным числам меньшим п и взаимно простым с т. Тогда < Zm *,·> - группа.
Доказательство. Опираясь на свойство взаимно простых чисел (если (а, т) = 1 и (b, т) = 1, то (а · b, т) = 1 и равносильность (a · b, m) = 1 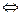 класс
класс 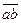 обратим, (см. лемму 2. 3. 6.) легко доказать, что умножение является бинарной алгебраической операцией в Zm *. Ассоциативность проверяется аналогично п. 1) доказательства теоремы 2. 3. 3. Класс
обратим, (см. лемму 2. 3. 6.) легко доказать, что умножение является бинарной алгебраической операцией в Zm *. Ассоциативность проверяется аналогично п. 1) доказательства теоремы 2. 3. 3. Класс 
 Zm играет роль единицы в Zm *. Обратимость элементов в Zm * следует из леммы 3. 5. 6.
Zm играет роль единицы в Zm *. Обратимость элементов в Zm * следует из леммы 3. 5. 6.
Определение 2. 3. 4. Количество натуральных чисел, меньших т и взаимно простых с т называется функцией Эйлера (и обозначается  (т)).
(т)).
Замечание. Очевидно, что | Zm * | =  (т).
(т).
Теорема 2. 3. 8. (Теорема Эйлера) Пусть (а, т) = 1, (а, т  N). Тогда
N). Тогда
a 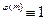 (mod m).
(mod m).
Доказательство. Пусть 
 Zm *. Имеем: | Zm * |
Zm *. Имеем: | Zm * | 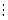 |
|  |, но | Zm * | =
|, но | Zm * | =  (т),поэтому
(т),поэтому  (т): |
(т): |  | или
| или  (т) = |
(т) = |  | · k (при некотором натуральном k). Тогда
| · k (при некотором натуральном k). Тогда
( )
) 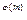 = (
= ( )
) 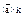 = (
= ( ) k =
) k =  . Равенство (
. Равенство ( )
) 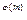 =
=  эквивалентно условию а
эквивалентно условию а 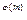
 1(mod m). Теорема Эйлера доказана.
1(mod m). Теорема Эйлера доказана.
Теорема Эйлера доставляет еще один способ вычисления обратного класса 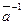 : если а и т взаимно просты, то
: если а и т взаимно просты, то 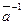 =
= 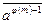 .
.
Пример. Вычислим класс 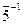 в Z 11. НОД (5, 11) = 1, так что класс
в Z 11. НОД (5, 11) = 1, так что класс 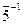 существует.
существует.  (11) = 10, поэтому
(11) = 10, поэтому 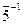 =
= 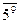 . Далее 52 =25
. Далее 52 =25  3 (mod 11)., возведем обе части сравнения в 4-ую степень:
3 (mod 11)., возведем обе части сравнения в 4-ую степень:
58  34 = 81
34 = 81  4 (mod 11), 59
4 (mod 11), 59  5 · 4 = 20
5 · 4 = 20  9 (mod 11). Итак,
9 (mod 11). Итак, 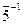 =
= 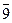 .
.
Теорема 2. 3. 9. Кольцо классов вычетов < Z m, +, · > является полем тогда и только тогда когда т - простое число.
Доказательство. Zт - коммутативное кольцо. Оно является полем, если содержит более одного элемента (т.е. т > 1), и для каждого ненулевого элемента в Zm существует обратный.
Если т - простое число, то все числа 1, 2,..., т - 1 взаимно просты с т, поэтому для каждого из ненулевых классов  ,
,  ,...,
,...,  существует обратный класс. Итак, в случае простого т кольцо Zm - поле.
существует обратный класс. Итак, в случае простого т кольцо Zm - поле.
Пусть т - составное число, т = ab, 1 < а < т. Тогда 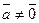 (а не делится на т) и НОД (а, т) = а
(а не делится на т) и НОД (а, т) = а 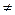 1, т. е. не существует обратного класса
1, т. е. не существует обратного класса 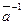 , и поэтому Zm не является полем. Теорема доказана.
, и поэтому Zm не является полем. Теорема доказана.
Теорема 2. 3. 10. (Теорема Вильсона). Натуральное число т 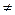 1 является простым тогда и только тогда, когда справедливо следующее сравнение:
1 является простым тогда и только тогда, когда справедливо следующее сравнение:
(m - 1)! + 1  0 (mod m).
0 (mod m).
Доказательство. Очевидно, что для составного числа т данное сравнение неверно. При т = 2 сравнение верно.
Пусть дано нечетное простое число т. В группе Zm *={  ,
,  ,...,
,...,  } только последний элемент имеет порядок 2. Поэтому все неединичные элементы, кроме
} только последний элемент имеет порядок 2. Поэтому все неединичные элементы, кроме  , разбиваются на пары взаимно обратных элементов. Следовательно, перемножая все элементы этой абелевой группы, мы получим
, разбиваются на пары взаимно обратных элементов. Следовательно, перемножая все элементы этой абелевой группы, мы получим  ! =
! = 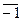 . Переходя от классов вычетов по модулю т к целым числам, получим требуемое сравнение.
. Переходя от классов вычетов по модулю т к целым числам, получим требуемое сравнение.
Лемма 2. 3. 11. Zm × Zn 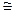 Zmn
Zmn 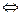 (m, п) = 1.
(m, п) = 1.
Доказательство. 1. Пусть g — образующий элемент в группе Zm,a h - образующий элемент в группе Zn и пусть r - порядок элемента ( g, h) в группе Zm × Zn. Так как ( g, h) mn = (gmn, hmn) = (e 1, e 2), то r 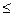 mn. А так как (gr, hr) = (g, h) r = (e 1, e 2), то r делится на m и на n. Если т и п взаимно просты, то получаем, что r = тп и (g, h) - образующий в группе Zm × Zn. Следовательно, Zm × Zn = Zmn.
mn. А так как (gr, hr) = (g, h) r = (e 1, e 2), то r делится на m и на n. Если т и п взаимно просты, то получаем, что r = тп и (g, h) - образующий в группе Zm × Zn. Следовательно, Zm × Zn = Zmn.
2. Если m и n не взаимно просты, то для их наименьшего общего кратного k имеем k < mn. Пусть k = mk 1 и k = nk 2. Если g и h – произвольные элементы групп Zm и Zn, то gm = e 1, hn = e 2. Поэтому
(g, h) k = (gmk1, hnk2) = (e1, e2).
Так как k < mn, то получаем, что в этом случае в группе Zm × Zn нет элементов порядка mn и, следовательно, группы Zm × Zn и Zm не изоморфны.
Теорема 2. 3. 12. (Теорема о мультипликативности функции Эйлера)  (m · n) =
(m · n) =  (m) ·
(m) ·  (n) для любых взаимно простых натуральных чисел m и n.
(n) для любых взаимно простых натуральных чисел m и n.
Доказательство.
 (m n) = | Z * mn | = |(Zm × Zn)*| = | Z * m × Z * n | = | Z * m | · | Z * n | =
(m n) = | Z * mn | = |(Zm × Zn)*| = | Z * m × Z * n | = | Z * m | · | Z * n | =  (m) ·
(m) ·  (n)
(n)
Здесь мы воспользовались тем, что | Z * mn | =  (m · n), | Z * m | =
(m · n), | Z * m | =  (m), | Z*n | =
(m), | Z*n | =  (n) и применим лемму 2. 3. 11.
(n) и применим лемму 2. 3. 11.
 2015-06-24
2015-06-24 3824
3824
