Нормальные подгруппы. Фактор-группы. Примеры

Теорема 2. 1. 1. Для подгруппы Н группы А эквивалентны утверждения:

1. Множество всех л.с.к. группы А по подгруппе Н замкнуто относительно умножения подмножеств.

2. Н замкнуто относительно взятия сопряжённых в А элементов, т.е. aha Н для любых h Н и а А.

3. аН = На для каждого а А.

4. Левостороннее и правостороннее разложения группы А по подгруппе Н совпадают.

Доказательство. 1 => 2. Т.к. аН ∙ а ^-1 Н = Н (теорема 1.4.2 п. 1.4.), то в силу свойства смежных классов 1) п. 1.4, аНа ^-1 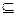Н. Это и означает, что Н имеете с каждым своим элементом h H содержит любой сопряжённый с ним элемент a ^-1 ha (a А).

2=>3. Поскольку аНа ^-1 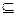Н и а ^-1 На = а ^-1 Н (а ^-1)^-1 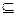Н, то аН 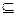На и На 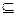аН, т.е. аН = На.

Очевидно, что 3 => 1. Ясно также, что 3 => 4. Докажем 4 =>3. Пусть левосторонние и правосторонние разложения группы А по подгруппе Н совпадают, т.е. в обоих случаях группа А есть объединение одних и тех же подмножеств. Поэтому л.с.к. аН совпадает с некоторым п.с.к. Нb,содержащим элемент а. По свойству 2) Нb = На. Значит, аН= На.

Определение 2. 1. 1. Подгруппа Н группы А называется нормальной подгруппой, если она удовлетворяет одному из эквивалентных условий 1 - 4 теоремы.

Употребительны названия - нормальный делитель, инвариантная подгруппа. Запись Н 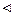А означает, что Н есть нормальный делитель A.

Теорема 2. 1. 2. Пусть Н 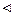А. Множество всех л.с.к. (п.с.к.) группы А но нормальной подгруппе Н относительно операции умножения подмножеств образует группу.

Доказательство непосредственно следует из опр. 2.1.1, теоремы 2.1.1 и теоремы 1.4.2.

Определение 2. 1. 2. Группа всех л.с.к. (п.с.к.) группы А по нормальной подгруппе Н называется фактор-группой группы А по нормальной подгруппе Н и обозначается А / Н.

Замечания: 1.Если группа А конечна, то по теореме Лагранжа | А / Н|= (А: Н) =| A |: | Н |.

2. Любая подгруппа абелевой группы нормальна.

Примеры фактор-групп

1. Для всякой группы А ее нормальными подгруппами будут тривиальные подгруппы Е = {е} и А. Разложение группы А по Е совпадает с разложением группы А на отдельные элементы, а разложение А по А состоит из одного смежного класса, равного А.

2. Пусть А = < M_nn (R), ∙ > - мультипликативная группа обратимых квадратных матриц п - го порядка с действительными элементами. Множество Н = { В M_nn (R) |В| = 1} обратимых матриц, принадлежащих определитель которых равен 1, будет мультипликативной подгруппой данной группы А. Найдем левостороннее разложение группы А по Н. Пусть М M_nn (R), тогда М ∙ Н = { М ∙ В_i | М M_nn (R), В_i Н). Так как В_i Н, то | В_i | = 1 и тогда |М ∙ В_i| = |М| ∙ | В_i | = | М| ∙ 1 = | М |, т.е. левый смежный класс, порожденный матрицей М, будет состоять из таких матриц, определители которых равны определителю матрицы М.

Найдем правый смежный класс, порожденный матрицей М.

Н ∙ М= { В_i ∙ М| В_i Н, M M_nn (R)}. | В_i ∙ М| = | В_i | ∙ |М| = 1 ∙ |М| = | М|. Таким образом ( M M_nn (R)) М ∙ Н =Н ∙ М, следовательно Н 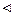А.

Фактор-группа А / Н состоит из классов матриц с одинаковыми ненулевыми определителями и фактически является мультипликативной группой R *.

3. Рассмотрим мультипликативную группу С * комплексных чисел. Отождествим С * с множеством точек плоскости без начала координат.

а) Н отождествим с прямой, проходящей через начало координат (без него). Тогда С * / Н - это пучок прямых, проходящих через начало координат, которые умножаются путём сложения их углов против часовой стрелки.

б) С* / С ¹ - это множество концентрических окружностей с центром в начале координат, которые умножаются путём перемножения их радиусов. Это даёт основание считать, что С */ С ¹ совпадает, по существу, с мультипликативной группой R⁺.

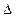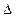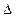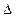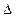4. Нормальными подгруппами группы G = { е, а, а ², b, а ∙ b, а ² ∙ b }симметрий правильного треугольника являются: Е = {е}, Н = { е, a, a ²}, G . Фактор-группы: G / Е = {{е}, { а },{ а ²},{ b }, { а ∙ b }, { а ² ∙ b }}; G / G 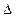= { G } G 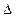/ Н = { { е, а, а² }, { b, а ∙ b, а ²∙ b }} = { Н, b ∙ Н }.

5. Нормальными подгруппами группы S ₃ = { = , = ,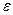

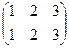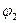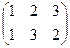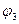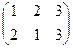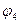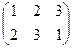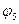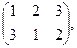
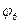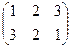= , = , = = } являются: Е = { },

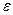A ₃ = { 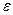, , 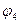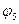} и S _3. Фактор-группы: S ₃ / E ={{ }, { }, { }, { },{ }, { }};

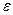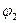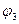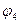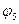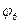S ₃ / S ₃ = { S ₃ }; S ₃/ A ₃ = {{ 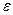, , 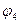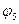}, { , 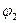, 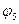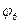}} ⁼ { A ₃, 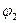∙ A ₃ }.