По определению, булев куб размерности n есть множество Вn ={<x1,x2,…,xn>|xk=0,1; k=1,2,…,n}. Элементы (точки) булева куба принять записывать в виде последовательности нулей и единиц, без запятых и скобок: x1x2…xn.
ê Булев куб является частично упорядоченным множеством:
a ´ b Ç аi ≤ bi для всех i=1,n.
ê Вектора 0 = (0, …,0) и 1 = (1,…,1) являются наименьшим и наибольшим элементами куба.
ê Этот порядок будем называть булевым порядком.
ê Булев куб с таким упорядочиванием является полной дистрибутивной решёткой.
ê Полная дистрибутивная решётка в то же время является и алгеброй типа <2,2,1>.
Алгеброй Буля называется алгебра, операции которой удовлетворяют следующим свойствам:
| Идемпотентность | aÙa = a | aÚa = a |
| Коммутативность | aÙb = bÙa | aÚb = bÚa |
| Ассоциативность | aÙ(bÙc) = (aÙb)Ùc | aÚ(bÚc) = (aÚb) Úc |
| Дистрибутивность | aÙ(bÚc) = (aÙb)Ú(aÙc) | aÚ(bÙc) = (aÚb)Ù(aÚc) |
| Законы нуля | aÙ0 = 0 | aÚ0 = a |
| Законы единицы | aÙ1 = 1 | aÚ1 = 1 |
| Свойства отрицания | aÙ(a) = 0 | aÚ(a) = 1 |
| Инволютивность | (a) = a | |
| Законы де Моргана | (aÙb) = (a)Ú(b) | (aÚb) = (a) Ù(b) |
| Законы поглощения | aÙ(aÚb) = a | aÚ(aÙb) = a |
| Законы склеивания | (aÚb)Ù(aÚb) = a | (aÙb)Ú(aÙb) = a |
| Двойственность | 0 = 1 | 1 = 0 |
ê Простейшая алгебра Буля B = (B; Ú, Ù,) имеет носителем двухэлементное множество B={0,1}, {Л, И} {F,T}, {^,¨}.
ê n–мерный булев куб является алгеброй Bn = (Bn; Ú, Ù,, 0,1).
ê n–мерный булев куб является полной дистрибутивной решёткой.
ê Алгебру Bn можно интерпретировать как векторное пространство над полем (B; Ú, Ù).
ê Алгебра Bn изоморфна алгебре (2U;Ç,È,¯,Æ,U) с n–элементным множеством U.
Точки булева куба представляются последовательностью (словом) длины n. Интерпретация этого слова как двоичного числа является нумерацией и, следовательно, задаёт на кубе линейный порядок, отличный от булева. Будем его называть числовым порядком.
n-мерный булев куб состоит из 2n элементов. Конечное число точек всегда можно изобразить на плоскости – т.е. булев куб произвольной размерности можно изображать графически.
Рассмотрим примеры.
n=0 n=1. – Двухэлементное множество, диаграмма Хассе которого имеет вид:
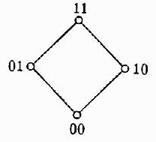
n=2. Булев квадрат имеет четыре элемента, изображаемые диаграммой:
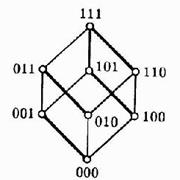
n=3. Трёхмерный булев куб изображается следующим образом:
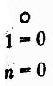
n=4. Четырёхмерный куб можно изобразить следующим образом:
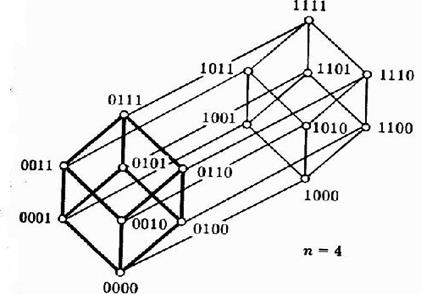
Этот же куб часто изображают в виде ориентированной сети. Линии сети соединяют элементы куба, находящиеся в отношении доминирования, а каждый слой (уровень) сети состоит из элементов антицепи.
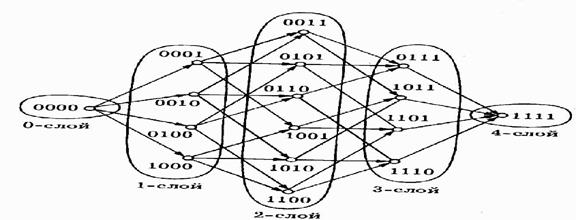
Грани булева куба.
Если в определении булева куба, т.е. множества всех двоичных векторов длины n, зафиксировать некоторую компоненту, скажем, k-ую, мы получим множество из 2n-1 элементов, которое будет изоморфно кубу размерности n–1. Это множество называется подкубом, или гранью, размерности n–1.
На подкубе индуцируется частичный порядок.
Номер зафиксированной компоненты называется направлением грани. Всего можно зафиксировать n различных компонент – говорят об n способах вложения или о соответствующем числе граней.
Продолжая процедуру фиксации компонент куба k раз, получим грань (подкуб) размерности n–k, номера зафиксированных компонент 1≤i1< … <ik≤n, определяющие направление грани, и значения (σ1, …, σk) зафиксированных компонент из множества {0,1}.
Грань размерности n–k – это множество наборов, имеющее не менее k одинаковых компонент. Грань данного куба задаётся: а) кортежем номеров (i1, …,ik) и б) значениями (σ1, …, σk).
Ребро – это грань размерности 1, т.е. подмножество куба, состоящее из двух элементов, один из которых доминирует над другим.
Параллельные грани.
 2015-06-24
2015-06-24 10260
10260
