Матроиды

Существование базиса в любом векторном пространстве принимается за аксиому. Практически важной задачей является выбор базиса E из некоторого множества векторов.

Алгоритм построения базиса. Пусть дано некоторое конечное множество векторов .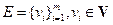

Выберем (произвольно) элемент v ₁ из Е. Положим v ₁ÎE. Выберем (опять произвольно) ещё один элемент из 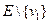. Проверим его на линейную независимость с v ₁. Если вектора независимы, добавим v ₂ в E. Если вектора зависимы, выбросим v ₂ из Е и найдём следующий 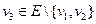и опять проверим на независимость. Если независим, то добавим его в E. Через конечное число шагов процедура закончится. На выходе получается система вложенных множеств линейно независимых векторов из Е: 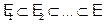. – Некоторая система подмножеств Е.

Результат зависит от правила (алгоритма) выбора векторов из Е.

Матроидом 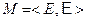называется конечное множество Е, | E |=n и семейство его подмножеств 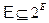таких, что:

М₁: 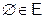(матроид не пуст);

М₂: ;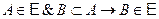

М₃: .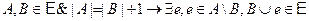

Примеры.

1. Семейства линейно независимых векторов – матричный матроид.

2. М= <E,2^E> – свободный матроид.

3. Матроид разбиений.

4. Матроид трансверсалей.

5. Матроид замыканий.

Циклы. Альтернативная система аксиом.

Эффективность матроидов.