2015-06-24
508
1. Пусть F = < F; +, ‰; 0, 1> – поле. Рассмотрим множество кортежей F n.Тогда F n= < F n;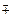 
> является абелевой (аддитивной) группой с операцией сложения
,
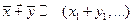нулем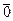 
= (0,…,0) и обратным (противоположным) элементом 
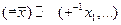. Если дополнить сложение векторов операцией покомпонентного умножения в поле F:
,
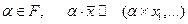то мы получим векторное пространство над F для любого конечного n. В частности, ¡n является векторным пространством для любого n.
Вопрос: чем отличается (геометрический) вектор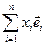 
в некотором базисе 
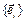и вектор (х 1,…, x n), составленный из его координат?
2. Булеан с симметрической разностью и «нулём»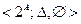 
является аддитивной абелевой группой. Если дополнительно ввести операцию умножения на скаляр:
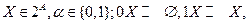
то булеан превратится в векторное пространство над полем ГалуаGF (2) (двоичной арифметикой Z2).
Если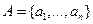 
, то векторы этого пространства, записанные в виде формальной суммы 
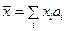, как подмножества могут быть выражены формулой 
.
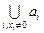Таким образом показано, что алгебру 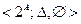можно рассматривать как некоторое векторное поле V.
|
|
|
3. Обобщение предыдущего.
Пусть F – некоторое поле,а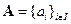 
– некоторое множество – м.б. конечным, счётным, континуальным (в этом случае индекс пробегает непрерывное множество),…
Образуем формальное выражение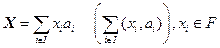 
.
Определим операции: сложения –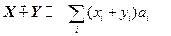 
и умножения на скаляр – 
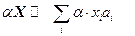, a Î F. Получаем векторное пространство над полем F,«натянутое на множество А».
4. Групповые алгебры
В качестве множества А из примера 3 возьмём группу G = {g1, …, gn}. Образуем линейное пространство L, элементами которого являются (формальные?) суммы вида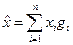 
, коэффициенты х являются элементами некоторого поля F. В поле F есть операции сложения и умножения на эти элементы. Таким образом, получается линейное пространство n измерений над группой G, или «натянутое на группу G», в котором, помимо линейных операций сложения и умножения в поле, определено действие группы: G: L a L по формуле 
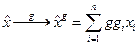(левые сдвиги). Эта формула есть определение гомоморфизма группы G в линейное пространство L. ––– Такой гомоморфизм называется представлением группы G на элементах линейного пространства L. Данная конструкция называется регулярным представлением группы.
Помимо линейных операций, на L можно определить бинарную (билинейную) операцию умножения L´LaL формулой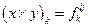 
, где справа стоит матрица из таблицы группового умножения.
Циклические и комплексные циклические числа получаются именно таким способом. К сожалению, умножение в алгебрах, построенных над циклическими группами, имеет делители нуля или сводится (изоморфизм!) к алгебре комплексных чисел.
5. Базис и размерность
· Кортежи вида (0,0,…,1,0,…0) образуют базис пространства F n, dim F n = n. Здесь F n – векторное пространство над полем F.
|
|
|
· Базисными векторами в примере 1 являются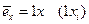 
· Одноэлементные подмножества образуют базис булеана. Т.е. любое подмножество множества А = { а 1, …, а n} может быть представлено в виде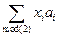 
. Отсюда следует, что dim(2А) = |А|.
