Тонкое полукольцо радиусом R равномерно заряжено с линейной плотностью + t и находится в вакууме. Определить силу взаимодействия полукольца с точечным зарядом + q0, находящимся в центре кривизны.
| Дано: R + t + q0 | Решение: Выделим элемент кольца dl, на котором находится заряд dq = tdl. Этот заряд является точечным, поэтому модуль силы взаимодействия зарядов dq и q0 находится по закону Кулона: 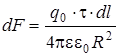 . . |
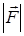 -? -? |
Разложим силу 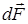 на составляющие
на составляющие 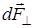 и
и 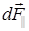 (рис.8). Поскольку полукольцо заряжено равномерно, то в силу симметрии сумма всех составляющих
(рис.8). Поскольку полукольцо заряжено равномерно, то в силу симметрии сумма всех составляющих 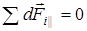 . Остаются только составляющие сил, пер-
. Остаются только составляющие сил, пер-
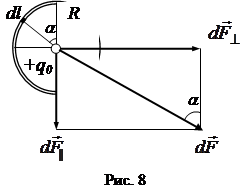 | пендикулярные диаметру полукольца. Поэтому опера- цию геометрического сложе- ния всех элементарных сил 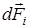 заменяем сложением их перпендикулярных составля- ющих, т.е. интегрированием. Составляющая заменяем сложением их перпендикулярных составля- ющих, т.е. интегрированием. Составляющая 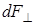 является величиной переменной, она зависит от угла a является величиной переменной, она зависит от угла a 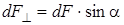 . . |
Поэтому интегрирование ведется по углу a в пределах от нуля до π.
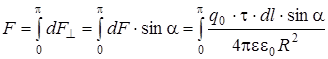
Элемент дуги окружности dl = R× da, тогда
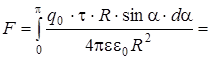
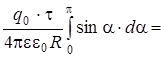
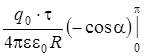 =
= 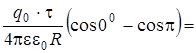
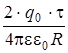 .
.
 2015-06-24
2015-06-24 2188
2188








