2015-06-24
560
Рассмотрим вспомогательный ряд, составленный из членов рядов (1) и (2):
.
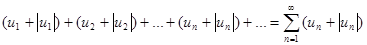Очевидно, что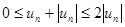 
для всех 
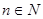. Но ряд 
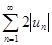сходится в силу условия теоремы и свойства чыисловых рядов. Следовательно, на основании признака сравнения сходится и ряд 
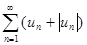. Поскольку данный знакопеременный ряд представляет собой разность двух сходящихся рядов 
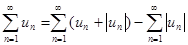, то, на основании свойства числовых рядов, ряд (1) сходится. Ч.т.д.
Определение. Ряд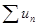 
называется абсолютно сходящимся, если сходится ряд из модулей его членов 
.
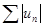Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают.
Определение. Ряд 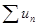называется условно сходящимся, если он сходится, а ряд из модулей его членов 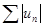расходится.
