Знакочередующимся рядом называется ряд вида:
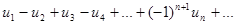 , где
, где 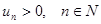
Признак Лейбница.
Знакочередующийся ряд сходится, если:
1. Последовательность абсолютных величин членов ряда монотонно убывает, т.е. 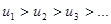 ;
;
2. Общий член стремится к нулю: 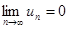 .
.
При этом сумма S ряда удовлетворяет неравенствам: 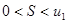 .
.
 2015-06-24
2015-06-24 634
634








