2015-06-24
664
Рассмотрим сначала частичную сумму четного числа (2m) членов ряда. Имеем
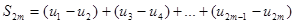
Выражение в каждой скобке, согласно первому условию теоремы, положительно. Следовательно, сумма S2m>0 и возрастает с возрастанием номера 2m.
С другой стороны, S2m можно переписать так:
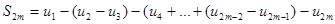
Легко видеть, что S2m<u1. Таким образом, последовательность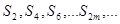 
возрастает и ограничена сверху. Следовательно, она имеет предел 
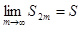, причем 
.
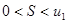Рассмотрим теперь частные суммы нечетного числа (2m+1) членов ряда. Очевидно, что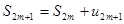 
. Отсюда следует, что 
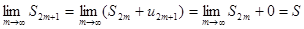, т.к. 
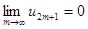в силу второго условия теоремы. Итак, 
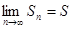как при четном n, так и при нечетном n. Следовательно, ряд сходится, причем 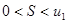. Ч.т.д.
Замечания:
1. Исследование знакочередующегося ряда вида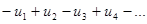 
сводится к стандартному путем умножения всех его членов на (-1);
2. Соотношение 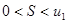позволяет получить простую и удобную оценку ошибки, которая допускается при замене суммы S данного ряда его частичной суммой Sn. Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд, сумма которого по модулю меньше первого члена этого ряда.
Определение. Числовой ряд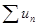 
содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Знакочередующийся ряд является его частным случаем.
Теорема. Пусть дан знакопеременный ряд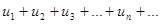 
(1). Если сходится ряд 
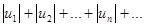(2) составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.
