2015-06-24
2936
Теорема. Если члены знакоположительного ряда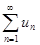 
могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке [1;¥) функции f(x) так, что u1= f(1), u2=f(2),…, un=f(n) …, то:
1) если несобственный интеграл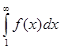 
сходится, то и ряд сходится;
2) если несобственный интеграл 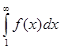расходится, то и ряд расходится.
Доказательство. Рассмотрим криволинейную трапецию, ограниченную сверху графиком функции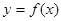 
, основанием которой служит отрезок оси Ох от х=1 до х=n.
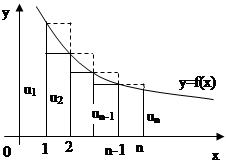Построим входящие и выходящие прямоугольники, основаниями которых служат отрезки [1;2], [2;3],.. Учитывая геометрический смысл определенного интеграла, запишем:
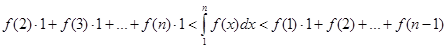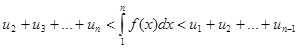или 
, или
.
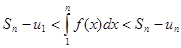Случай 1. Несобственный интеграл 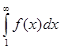сходится, т.е. 
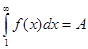. Поскольку 
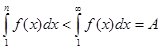, то с учетом неравенства имеем Sn-u1<A, т.е. Sn<A+u1. Так как последовательность частичных сумм монотонно возрастает и ограничена сверху, то, по признаку существования предела, имеет предел. Следовательно, ряд сходится.
Случай 2. Несобственный интеграл 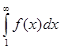расходится. Тогда 
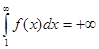и интегралы 
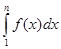неограниченно возрастают при 
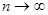. Учитывая, что 
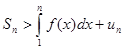, получаем, что 
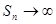при 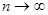. Следовательно, данный ряд расходится. Ч.т.д.
Пример. Рассмотрим ряд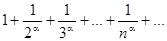 
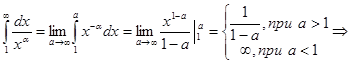сходится при a>1 и расходится a£1. Ряд 
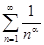называется общегармоническим рядом.
Пример. Исследовать на сходимость ряд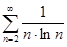 
.
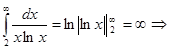ряд расходится.
Следствие. Если f(x) и j(х) – непрерывные функции на интервале (a, b] и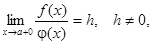 
то интегралы 
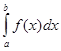и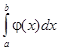 
ведут себя одинаково в смысле сходимости.
