Конечно-элементная реализация

Конечно-элементная дискретизация, в основном, выполняется обычным образом, за исключением некоторых специальных требований в связи с поверхностью 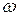. Вся область 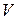разбивается на конечные элементы таким образом, чтобы поверхность 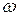была аппроксимирована сторонами примыкающих к ней конечных элементов, соответствующие узлы которых со стороны подобласте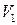й и 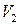совпадали бы друг с другом. Чтобы иметь возможность реализовать негладкие условия контакта, занумеруем узлы конечно-элементной сетки, принадлежащие границе 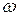, дважды таким образом, чтобы один номер относился к области 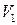, а другой – к .

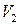После обычной процедуры конечно-элементной дискретизации получим систему линейных алгебраических уравнений:

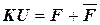, (3)

где 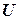– искомый вектор узловых перемещений, 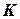– матрица жесткости, 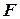– обычный вектор усилий, в который в соответствии с функционалом (2) входят узловые значения векторов объемных и поверхностных усилий, 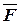– вектор узловых значений, отвечающий заданному значению скачка усилий на поверхности .

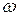К системе (3) следует добавить два уравнения, обусловленные заданными кинематическими условиями – заданными перемещениями на границах 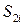и заданным скачком вектора перемещений на границе :

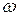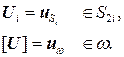
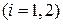(4)

Конечно-элементная реализация скачка в усилиях приводит к появлению дополнительного слагаемого в правой части результирующей СЛАУ, т.е. реализуется аналогично обычным краевым условиям в усилиях. В то время как реализация скачка в перемещениях требует изменения и матрицы, и вектора правых частей результирующей СЛАУ.

Техника реализации скачка в перемещениях хотя и похожа на реализацию кинематических краевых условий, так как в некоторой степени означает исключение соответствующих неизвестных из результирующей СЛАУ, однако может быть выполнена по-разному. В работе рассмотрен способ, сохраняющий размерность и симметричность матрицы СЛАУ.

Не умаляя общности, предположим, что:

· все номера узлов области 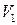меньше номеров узлов области .

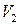· номера узлов, принадлежащих границе 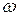, являются последними номерами в области 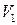и первыми в области .

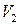· рассматривается реализация для однородного скачка 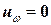, так как значение скачка не влияет на изменения в матрице СЛАУ, а из контекста производимых операций будет понятно, когда данные изменения коснутся вектора правых частей.

В условиях данных предположений, глобальная матрица задачи будет представлять собой прямую сумму глобальных матриц, соответствующих областям 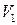и 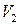, т.е. будет иметь вид:

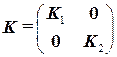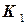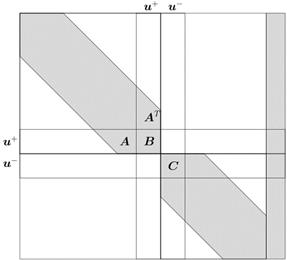
При должной нумерации узлов глобальные матрицы и 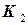будут иметь ленточную структуру, тогда расширенную матрицу задачи можно изобразить, как показано на рис. 1(а), и она состоит из двух частей: собственно матрицы СЛАУ и вектора правых частей, который обозначен столбцом серого цвета справа от матрицы СЛАУ. Белым цветом обозначены места заведомых нулей в матрице СЛАУ, а серым – места, на которых могут быть ненулевые элементы матрицы СЛАУ и вектора правых частей.

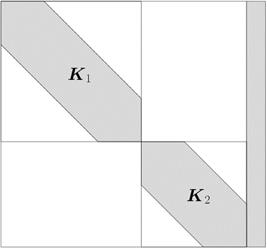
(а) (б)

Рис.1. Расширенная матрица СЛАУ.

Выделим столбцы и строки в расширенной матрице СЛАУ, которые соответствуют принадлежащим границе 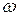узлам, при этом обозначим через 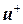узлы, принадлежащие области 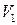, а через 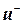– узлы, принадлежащие области 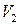, как показано на рис. 1(б). Учитывая симметричность матрицы СЛАУ, выделим некоторые части матрицы, обозначив их буквам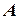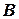и , и 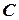, как показано на рис. 1(б).

Тогда в принятых обозначениях условие скачка в перемещениях может быть записано в следующем виде:

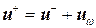. (5)

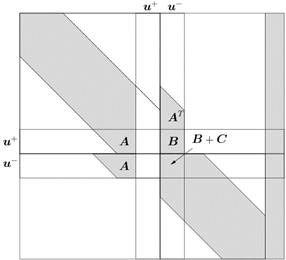
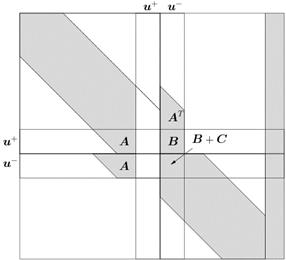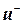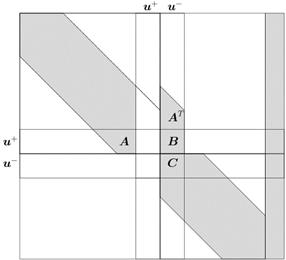
Подставим уравнения (5) в систему (3) (система после преобразования показана на рис. 2(а)), после чего прибавим к уравнениям, отвечающим узлам , уравнения соответствующие узлам 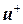, тогда расширенная матрица СЛАУ преобразуется к виду, показанному на рис. 2(б).

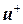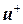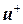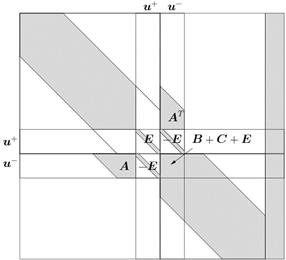
После данных преобразований неизвестные, соответствующие узлам , были исключены из системы, поэтому можно «вычеркнуть» строки и столбцы, отвечающие узлам . В решение преобразованной СЛАУ входят все компоненты искомого вектора перемещений кроме компонент, отвечающих узлам . Для определения данных компонент, вместо изначальных уравнений СЛАУ, соответствующих неизвестным 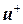, запишем совокупность уравнений скачка (5). Тогда расширенная матрица СЛАУ примет вид, показанный на рис. 3(а). Здесь введено еще одно обозначение для части матрицы СЛАУ – 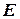. Такое обозначение выбрано из-за того, что в конкретном примере (при данных глобальной и локальной нумерациях) данная часть матрицы СЛАУ будет иметь вид единичной матрицы.

(а) (б)

Рис.2. Исключение части неизвестных из СЛАУ.

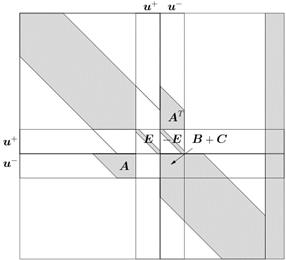
Последним шагом будет восстановление симметричности матрицы СЛАУ. Для этого достаточно вычесть из уравнений, соответствующих узлам 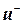, уравнения, отвечающие узлам 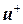. Тогда расширенная матрица СЛАУ примет вид, показанный на рис. 3(б).

Таким образом, после учета скачка в перемещениях матрица СЛАУ сохранила порядок и симметричность.

Отметим, что матрица СЛАУ, на которой проводилось объяснение алгоритма учета скачка в перемещениях, была специально выбрана ленточной и блочно-диагональной для наглядности. При решении задач глобальная и локальная нумерации узлов могут быть выбраны не оптимальным образом, однако, на сам алгоритм учета скачка, его корректность и свойства нумерация узлов не влияет.