Решение тестовой задачи в пакете ANSYS

В работе было рассмотрено несколько способов программного взаимодействия с пакетом ANSYS, и был выбран суперэлементный подход. В данном подходе взаимодействие с пакетом ANSYS осуществляется через бинарные файлы суперэлементов, которые ANSYS создает в процессе решения любой задачи, в модели которой присутствует хотя бы один суперэлемент.

Суперэлемент в МКЭ представляет собой группу конечных элементов, которые рассматриваются как один элемент с выбранным набором главных степеней свободы. В пакете ANSYS суперэлемент полностью определяется своим бинарным файлом, в который помимо общей информации о геометрии, нумерации степеней свободы, входящих в суперэлемент, и прочего, хранятся матрицы жесткости, масс, демпфирования и векторы нагрузок суперэлемента в явном виде [6].

Основным преимуществом данного подхода является наличие предоставляемых пакетом ANSYS функций для программного создания, чтения и модификации бинарных файлов суперэлементов [7].

В качестве тестовой задачи рассмотрена задача определения напряженно-деформированного состояния плоской упругой области, протяженной в горизонтальном направлении и содержащей границу 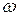, которая делит ее на две части (левая часть – 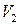, а правая – 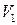), возможно, имеющие разные механические характеристики (рис. 4). На 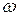задан скачок в перемещениях; скачок в напряжениях полагается равным нулю.

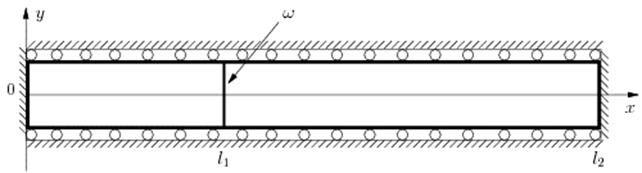
Рис. 4. Расчетная область с заданными скачками перемещений на границе .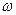

Однородные краевые условия на границе расчетной области и скачок задаются таким образом, чтобы в задаче была симметрия относительно горизонтальной осевой линии. В этом случае решение тестовой задачи относительно 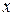-овых компонент решения с хорошей степенью точности может быть аппроксимировано решением соответствующей одномерной задачи:

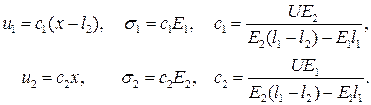
Здесь 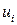, 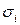– перемещения и напряжения в области 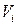; 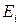– модуль упругости в области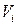 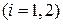; 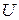– заданный скачок в перемещениях на границе 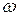; 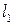, 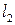– длина левой части области и протяженность всей области соответственно.

При моделировании расчетной области в пакете ANSYS выполнено условие двойной нумерации узлов, принадлежащих границе 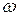. В качестве суперэлемента выбраны два слоя конечных элементов, аппроксимирующих границу 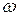, – один слой элементов принадлежит области 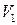, а другой – .

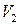После стандартной процедуры создания суперэлемента и записи его бинарного файла, последний модифицируется необходимым образом с помощью разработанной программы, которая считывает из бинарного файла матрицу жесткости и вектор нагрузок суперэлемента, преобразует их с учетом скачка в перемещениях и записывает обратно в файл уже измененные матрицу жесткости и вектор нагрузок. Модифицированный суперэлемент, в котором уже учтен скачок в перемещениях используется для решения исходной задачи. Данный этап решения не отличается от решения стандартной задачи, содержащей суперэлемент как часть расчетной модели.

Результаты решения в пакете ANSYS поставленной задачи хорошо согласуются с аналитическим решением.