Постановка задачи. В работе рассматривается внедрение в пакет ANSYS конечно-элементных алгоритмов решения задач теории упругости с заданными скачками искомых функций

РЕШЕНИЕ СТАТИЧЕСКИХ ЗАДАЧ ТЕОРИИ УПРУГОСТИ С ЗАДАННЫМИ СКАЧКАМИ ИСКОМЫХ ФУНКЦИЙ В ПАКЕТЕ ANSYS

Введение

В работе рассматривается внедрение в пакет ANSYS конечно-элементных алгоритмов решения задач теории упругости с заданными скачками искомых функций. Подобные задачи возникли в теории сейсмостойкости массивных сооружений, где такие постановки были получены путем математически строгих преобразований [1-3].

Задание условий контакта в виде заданного скачка перемещений и напряжений не реализовано в пакете ANSYS, поэтому решение подобных задач стандартными средствами пакета невозможно.

Расширение возможностей пакета ANSYS путем включения в него новых алгоритмических возможностей представляется наиболее привлекательной формой использования данного пакета для исследовательских работ, поскольку означает изучение новых содержательных, математических, численных и алгоритмических моделей, одновременно используя функциональный интерфейс, современные структуры данных, мощные решатели и возможности пре- и постпроцессора пакета.

В работе рассматриваются статические задачи теории упругости с заданными скачками искомых функций, что имеет теоретический интерес. Цель работы показать принципиальную возможность включения алгоритмов для задач с заданными скачками в пакет ANSYS.

Постановка задачи

Рассмотрим статическую задачу теории упругости с заданными скачками искомых функций. Пусть рассматриваемая область 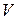разделена поверхностью 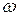так, что 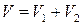и 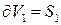, , 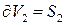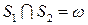. Поверхность 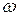предполагается достаточно гладкой. Запишем дифференциальную постановку задачи [4], используя матрично-векторные обозначения [5] удобные для перехода к конечно-элементной дискретизации:

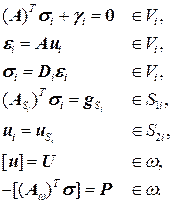
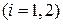(1)

Квадратными скобками здесь обозначен скачок стоящей в скобках величины при переходе через границу контакта областей, например,

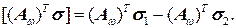
Прежде чем привести выражение функционала для задачи с заданными скачками искомых функций, отметим одну особенность, связанную с представлением скачка произведения скалярных функций, если эти функции в одной и той же точке претерпевают заданный разрыв первого рода. Пусть имеются две функци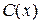и и 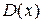, каждая из которых может претерпевать конечных разрыв в точке 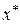. Обозначим 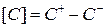и 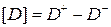. Скачок произведения функци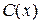й и 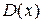в точке 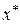может быть представлен неединственным образом. Легко непосредственно проверить, что общий вид такого представления будет:

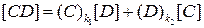
для любых 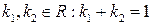, где

, .

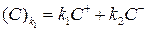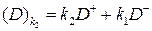Аналогичные соотношения имеют место в случае рассмотрения векторных функций.

Очевидно, что вариационные постановки, то есть вариационные уравнения и функционалы для статических задач с заданными скачками искомых функций, будут отличаться от обычных наличием интегралов по границе контакта областей 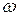[4]. Под этими интегралами будут стоять как раз произведения векторов перемещений и усилий на границе 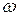, остальные части этих постановок имеют обычный вид. Например, если обозначить через 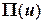функционал Лагранжа в задаче без скачков перемещений и усилий, а через 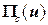– функционал Лагранжа в задаче со скачками, то

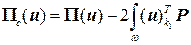
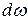. (2)

В функционал (2) могут входить различные численные величины 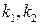, удовлетворяющие условию 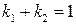. Очевидно, что отвечающие этим функционалам уравнения Эйлера, равно как и решения самих задач со скачками, от 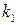и 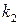зависеть не будут.