Вверх
В компьютерах для записи чисел используется двоичная система счисления. В этой системе для представления любого числа используются два символа — цифры 0 и 1. Основание системы счисления 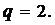
Произвольное число с помощью формулы можно представить в виде разложения по степеням двойки:
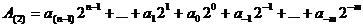 (3.3)
(3.3)
Таким образом, все числа в двоичной системе счисления составляются из цифр 0 или 1. Например, 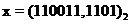 . Двоичное представление числа требует примерно в 3,3 раза большего числа разрядов, чем его десятичное представление. Тем не менее, применение двоичной системы счисления создает большие удобства для работы ЭВМ, так как для представления в машине разряда двоичного числа может быть использован любой запоминающий элемент, имеющий два устойчивых состояния.
. Двоичное представление числа требует примерно в 3,3 раза большего числа разрядов, чем его десятичное представление. Тем не менее, применение двоичной системы счисления создает большие удобства для работы ЭВМ, так как для представления в машине разряда двоичного числа может быть использован любой запоминающий элемент, имеющий два устойчивых состояния.
Арифметические действия над одноразрядными двоичными числами выполняются по следующим правилам:
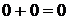
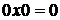
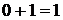
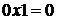
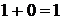
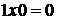
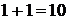
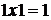
(3.4)
ЭВМ работают с двоичными кодами, пользователю удобнее иметь дело с десятичными или шестнадцатеричными кодами. Возникает необходимость перевода числа из одной системы счисления в другую.
Допустим, число A из системы счисления с основанием q требуется перевести в систему счисления с основанием 2.
Перевод целой части числа. При переводе целой части числа из десятичной системы счисления в двоичную систему счисления применяется метод последовательного деления на число 2, равное основанию новой системы счисления. Полученное частное сравнивается с делителем. Если частное больше делителя, то теперь уже частное делим на основание системы. И так до тех пор, пока частное не станет меньше делителя 2. Результат формируется путем последовательной записи последнего частного и всех без исключения остатков деления начиная с последнего.
Пример. Число 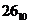 перевести в двоичную систему счисления.
перевести в двоичную систему счисления.
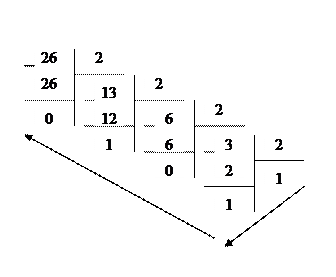
Перевод выполним по следующей схеме:
в результате 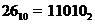 .
.
Для перевода числа из системы счисления с основанием 2 в десятичную, следует сложить все степени с основанием 2, соответствующие позициям разрядов исходного 2-го исла, в которых цифры равны 1.

Пример: Число 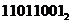 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
Представим исходное число в виде:
Перевод дробных чисел. При переводе дробной части числа применяется метод последовательного умножения на число, равное основанию новой системы счисления.
Перевод осуществляется по следующему правилу:
- исходное число умножаем на новое основание 2;
- полученная при этом целая часть произведения является первой искомой цифрой;
- дробную часть снова умножаем на основание 2 т.д.
Результат формируется путем последовательной записи целых частей произведения, начиная с первого.
Пример. Перевести число 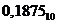 в двоичную систему
в двоичную систему
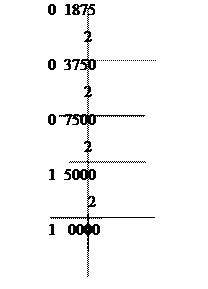
Здесь вертикальная черта отделяет целые части чисел от дробных частей. Результат: 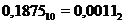 .
.
Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой).
Пример. Перевести десятичное число 105,1875 в двоичную систему счисления.
Результат: 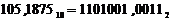 .
.
 2015-06-26
2015-06-26 3365
3365
