Методические указания. Раздел 1. Математические основы построения дискретных систем автоматики

Раздел 1. Математические основы построения дискретных систем автоматики

СОДЕРЖАНИЕ ДИСЦИПЛИНЫ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Системы счисления. Двоичный, десятичный, восьмеричный, шестнадцатеричный коды. Перевод из одной системы счисления в другую.

Двоичная арифметика. Устройства для выполнения арифметических операций. Сумматоры. Представление отрицательных чисел. Сдвиговые регистры.

Литература: [1].

Следует уяснить, что Системой счисления называется совокупность цифровых знаков и правил их записи, применяемая для однозначного изображения чисел.

Позиционными называются такие системы, в которых применяется ограниченный набор цифр, причем значение каждой цифры находится в строгой зависимости от ее позиции в числе. Количество различных цифр, применяемых в данной системе, называется ее основанием.

На пример десятичная система, в ней применяются десять цифр: О, 1, 2, 3, 4, 5, 6, 7, 8, 9; поэтому ее основанием является число десять. Произвольное десятичное число 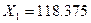, можно представить в следующем виде: 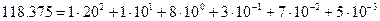. В левой части равенства записано символическое изображение числа. Правая часть равенства показывает, что все цифры числа в разных позициях имеют разный вес. Каждая позиция с присвоенными ей номером и весом называется разрядом числа. В частности, единица в первом разряде означает сотню, а единица во втором разряде — только десяток. Анализ; структуры числа 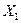показывает, что любое десятичное число' может быть представлено в виде суммы попарных произведений:

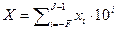(1)

где 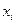= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} — некоторая цифра данной системы; J — количество разрядов в целой части числа (до запятой); F — количество разрядов в дробной части числа (после запятой); 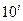— разрядный вес некоторой цифры.

В определении позиционных систем счисления не наложено никаких ограничений на величину основания. Отсюда очевидно, что основанием системы счисления может быть не только число десять, но и любое другое целое число. При этом структурно некоторое число в другой системе счисления также будет состоять из суммы по парных произведений цифр и степеней основания системы. Если основанию новой системы присвоить по аналогии с числом десять обозначение 10, то формула (1|) будет справедливой для записи чисел в любой системе счисления. В частности, можно, например, рассмотреть. двоичную систему счисления, основанием которой является число два, и, следовательно, для изображения чисел применяются всего две цифры: 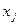={0, 1}. Основание системы счисления два можно записать с помощью имеющихся цифр только одним способом, т. е. в виде числа 10. Таким образом, любое число в двоичной системе записывается в виде комбинации нулей и единиц, расставленных согласно формуле (1). Так, уже рассмотренное нами десятичное число 118,375 в двоичной системе запишется следующим образом: 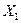=1110110,011 =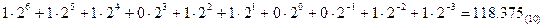. Индекс в круглых скобках показывает величину основания системы, в которой записано данное число.

Используя формулу (1), можем записать это же число в восьмеричной системе счисления: 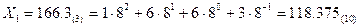. Для изображения чисел в этой системе применяются восемь цифры: 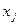={0, 1,2,3,4,5,6,7}.

Используя формулу (1), так же можем записать это же число в шестнадцатеричной системе счисления: 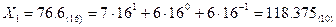Эта система состоит из 16 цифр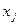={0, 1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}.