Вверх
Восьмеричная система счисления. Числа, записанные в системе с основанием 8, называются восьмеричными. Основание системы счисления - q = 8. Изображение чисел производится восьмью цифрами: {0, 1, 2, 3, 4, 5, 6, 7}. Восьмеричная система счисления используется в ЭВМ для кодирования команд в целях сокращения записи.
Шестнадцатеричная система счисления. Основание системы счисления - q = 16. В шестнадцатеричной системе счисления алфавит включает в себя 16 символов (цифры и буквы): { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F}. Широко применяется для написания кодов операций констант и других специальных слов, не требующих перевода в десятичную систему счисления. В таблице 3.1 приведен алфавит для четырех систем счисления.
Таблица 3.1 - Алфавит систем счисления.
| Основание | Название | Алфавит |
| двоичная | 0 1 | |
| восьмеричная | 0 1 2 3 4 5 6 7 | |
| десятичная | 0 1 2 3 4 5 6 7 8 9 | |
| шестнадцатеричная | 0 1 2 3 4 5 6 7 8 9 A B C D E F |
Любое число по специальным правилам можно перевести из одной системы счисления в другую. Рассмотрим эти правила.
Допустим, число Х из системы счисления с основанием q требуется перевести в систему счисления с основанием p. Числа, имеющие целую и дробные части, переводятся в два этапа: вначале целая часть числа, а затем дробная.
Перевод целых чисел из одной системы счисления в другую осуществляется по следующему правилу:
- целую часть числа делим на новое основание p;
- полученный от деления первый остаток является младшей цифрой целой части числа с основанием р;
- деление будем производить до тех пор, пока не получим частное меньше делителя;
- последнее частное дает старшую цифру числа с основанием р.
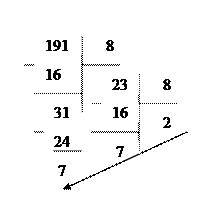
Пример. Число 19110 перевести в восьмеричную систему счисления.
Перевод осуществим методом последовательного деления десятичного числа 191 на 8. Остатки от деления образуют восьмеричное число:
в результате 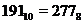 .
.
Перевод дробных чисел из одной системы счисления в другую. Предположим, что правильную дробь Х, представленную в системе с основанием q, требуется перевести в систему счисления с основанием р. Перевод осуществляется по следующему правилу:
- исходное число умножаем на новое основание р;
- полученная при этом целая часть произведения является первой искомой цифрой;
- дробную часть снова умножаем на основание р и т.д.
Пример. Перевести число 0,187510 в восьмеричную и шестнадцатеричную системы.
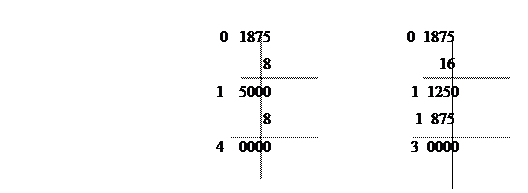
Здесь вертикальная черта отделяет целые части чисел от дробных частей. Результат: 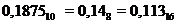 .
.
Перевод из двоичной в восьмеричную и шестнадцатеричную систему счисления и обратно. Восьмеричная и шестнадцатеричная системы счисления являются вспомогательными системами при подготовке задачи к решению. Удобство ее использования состоит в том, что числа соответственно в 3 и 4 раза короче двоичной системы, а перевод в двоичную систему и обратно несложен и выполняется простым механическим способом.
Для того чтобы произвольное двоичное число записать в системе счисления с основанием 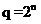 , нужно:
, нужно:
n данное двоичное число разбить слева и справа (целую и дробную части) на группы по n цифр в каждой;
n если в последних правой и левой группах окажется меньше n разрядов, то их надо дополнить справа и слева нулями до нужного числа разрядов;
n рассмотреть каждую группу как n - разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием 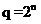 .
.
Значит для того чтобы произвольное число записать в системе счисления с основанием 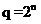 , т. е. перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-разрядным эквивалентом в двоичной системе счисления. Применительно к компьютерной информации часто используются системы счисления с основанием 8 (восьмеричная) и 16 (шестнадцатеричная).
, т. е. перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-разрядным эквивалентом в двоичной системе счисления. Применительно к компьютерной информации часто используются системы счисления с основанием 8 (восьмеричная) и 16 (шестнадцатеричная).
Перевод двоичных чисел в восьмеричную систему счисления. Для того чтобы двоичное число записать в восьмеричной системе счисления, необходимо разбить его на триады (т.е. группы по 3 цифры, так как 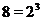 ), начиная от запятой, отделяющей целую часть от дробной части. После этого каждая триада заменяется одной соответствующей ей восьмеричной цифрой. Недостающие справа и слева цифры восполняются нулями. Связь между двоичной и восьмеричной системами счисления приведена в таблице 3.2. Каждой восьмеричной цифре соответствует тройка двоичных чисел.
), начиная от запятой, отделяющей целую часть от дробной части. После этого каждая триада заменяется одной соответствующей ей восьмеричной цифрой. Недостающие справа и слева цифры восполняются нулями. Связь между двоичной и восьмеричной системами счисления приведена в таблице 3.2. Каждой восьмеричной цифре соответствует тройка двоичных чисел.
Таблица 3.2 - Двоично-восьмеричная таблица
| 8 – ричная система счисления | 2 –ичная система счисления |
Пример. Перевести число 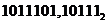 в восьмеричную систему счисления.
в восьмеричную систему счисления.
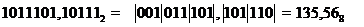
Перевод двоичных чисел в шестнадцатеричную систему счисления. Для того чтобы двоичное число записать в 16-ричной системе счисления, необходимо разбить его на тетрады (группы из 4 цифр, т.к. 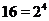 ), начиная от запятой, в обе стороны. После этого каждая тетрада заменяется соответствующей ей 16-ричной цифрой. В этом случае используется двоично-шестнадцатеричная таблица.
), начиная от запятой, в обе стороны. После этого каждая тетрада заменяется соответствующей ей 16-ричной цифрой. В этом случае используется двоично-шестнадцатеричная таблица.
Таблица 3.3 - Двоично-шестнадцатеричная таблица.
| 16 – ричная система счисления | 2 – ичная система счисления | 16 – ричная система счисления | 2 – ичная система счисления |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
Пример Перевести число 1011101,101112 в шестнадцатеричную систему счисления.
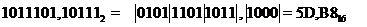
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления. Для перевода 8-ричного числа в двоичную систему счисления достаточно каждую восьмеричную цифру заменить соответствующей ей двоичной триадой. Для перевода 16-го числа в двоичную систему счисления достаточно каждую шестнадцатеричную цифру заменить соответствующей ей двоичной тетрадой.
Пример. Число 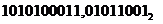 перевести в шестнадцатеричную систему счисления и восьмеричную.
перевести в шестнадцатеричную систему счисления и восьмеричную.
Перевод осуществляется следующим образом:
| 0011, | ||||
| А |
т.е. 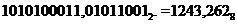
| 011, | ||||||
т.е. 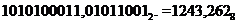
При переходе из 8-ричного счисления в 16-ричное счисление и обратно используется вспомогательный, двоичный код числа.
Пример. Перевести число 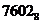 перевести в 16-ичное счисление, 1CD,
перевести в 16-ичное счисление, 1CD, 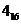 в 8–е счисление
в 8–е счисление
7 6 0 2 F 8 2
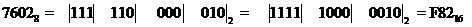
С E 4 5 6 7 6 3 4
1 C D 4 7 1 5 2
3.2 Формы представления и преобразования информации
3.2.1 Кодирование и форматы представления числовых данных
3.2.2 Кодирование и формат представления символьной информации
 2015-06-26
2015-06-26 929
929








