6.1. Элементы комбинаторики:
Определение:
Соединения, содержащие 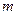 элементов из данных
элементов из данных  и отличающиеся друг от друга либо сами элементами, либо порядком их расположения в соединениях называются размещениями.
и отличающиеся друг от друга либо сами элементами, либо порядком их расположения в соединениях называются размещениями.
Формула вычисления: 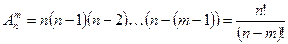
Определение:
Соединения, содержащие все данные  элементов и отличающиеся друг от друга только порядком расположения элементов, называются перестановками из
элементов и отличающиеся друг от друга только порядком расположения элементов, называются перестановками из  элементов.
элементов.
Формула вычисления: 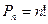
Определение:
Соединения, содержащие 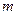 элементов из данных
элементов из данных  и отличающиеся друг от друга хотя бы одним элементом назвыаются сочетаниями из
и отличающиеся друг от друга хотя бы одним элементом назвыаются сочетаниями из  элементов по
элементов по 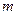 .
.
Формула вычисления: 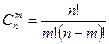 .
.
В частности, если 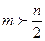 , то
, то 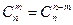 .
.
6.2. Основные понятия теории вероянтостей:
Изначальные понятия: событие и вероятность.
Под событием понимают всякий факт, относительно которого уместно говорить: произойдет оно или нет.
События делят на: случайные, достоверные и невозможные.
Определение:
Случайным событием называют всякое явление, которое в результате ОКУ может произойти или не произойти.
Обозначение: 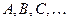
Определение:
Событие называется достоверным, если оно заведомо происходит при ОКУ.
Обозначение: 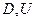 .
.
Определение:
Событие называется невозможным, если оно заведомо не происходит при ОКУ.
Обозначение: 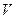
Определение:
Несколько событий называются равновозможными, если ни одно из них не является объективно более возможным, чем любое другое.
Определение:
Несколько событий называются несовместными, если появление одного из них исключает появление любого другого и совместными, если не исключает.
Определение:
Несколько событий образуют полную группу, если в результате ОКУ обязательно происходит хотя бы одно из данных событий.
Определение (классическое определение вероятностей):
Если в результате ОКУ всевозможные исходы составляют полную группу  и равновозможных и несовместных случаев, из которых
и равновозможных и несовместных случаев, из которых 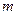 благоприятствуют появлению события
благоприятствуют появлению события  , то вероятность этого события равна отношению числа благоприятствующих событий к их общему числу.
, то вероятность этого события равна отношению числа благоприятствующих событий к их общему числу.
Т.о. 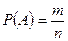 .
.
Определение:
Два события 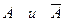 называются противоположными, если в результате ОКУ обязательно происходит одно и только одно из них.
называются противоположными, если в результате ОКУ обязательно происходит одно и только одно из них.
Теорема: 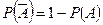 .
.
6.3. Теоремы сложения и умножения:
Определение:
Произведением двух событий называется событие, состоящее в их одновременном появлении.
Обозначение: 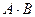
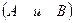 .
.
Определение:
Два события 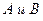 называются независимыми, если вероятность любого из них не зависит от того, произошло или не произошло другое событие и зависимыми, если зависит.
называются независимыми, если вероятность любого из них не зависит от того, произошло или не произошло другое событие и зависимыми, если зависит.
Определение:
Вероятность события 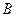 , вычисленная при условии, что событие
, вычисленная при условии, что событие  произошло, называется условной вероятностью события
произошло, называется условной вероятностью события 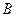 .
.
Обозначение: 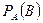 или
или 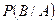 .
.
Определение:
Вероятность события 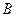 , вычисленная без учета появления, или не появления
, вычисленная без учета появления, или не появления  называется безусловной вероятностью события
называется безусловной вероятностью события 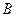 .
.
Обозначение: 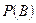 .
.
Теорема умножения:
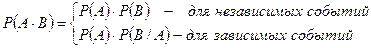
Замечание: теорема остается справедливой и для большего количества событий.
Определение:
Суммой двух событий  и
и 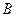 называется событие, состоящее в том, что появится хотя бы одно из этих событий.
называется событие, состоящее в том, что появится хотя бы одно из этих событий.
Обозначение: 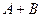
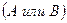 .
.
Теорема сложения:
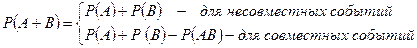 .
.
Замечание: теорема остается справедливой и для большего количества событий.
Следствия:
- Сумма вероятностей несовместных событий, образующих полную группу, равна единице, т.е. 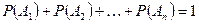 ;
;
- 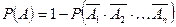 - формула расчета вероятности появления хотя бы одного из
- формула расчета вероятности появления хотя бы одного из  совместных событий.
совместных событий.
Теорема (формула полной вероятности):
Если случайные гипотезы 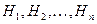 образуют полную группу несовместных событий и событие
образуют полную группу несовместных событий и событие  может произойти только после наступления одной из гипотез, то вероятность появления события
может произойти только после наступления одной из гипотез, то вероятность появления события  рассчитывается по формуле
рассчитывается по формуле
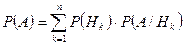 .
.
Теорема (гипотез или формула Бейеса):
Пусть случайные гипотезы 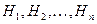 образуют полную группу несовместных событий, известны вероятности появления этих гипотез
образуют полную группу несовместных событий, известны вероятности появления этих гипотез 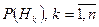 , событие
, событие  уже произошлою, то
уже произошлою, то 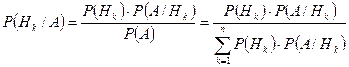 .
.
Повторение испытаний:
- Если 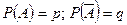 , то
, то 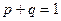 ;
;
- В  независимых испытаниях событие
независимых испытаниях событие  появится хотя бы один раз с вероятностью
появится хотя бы один раз с вероятностью 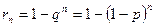 .
.
Теорема (формула Бернулли):
Если проводится  независимых испытаний, в результате каждого из которых событие
независимых испытаний, в результате каждого из которых событие  может появится с вероятностью
может появится с вероятностью 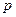 и не появится с вероятностью
и не появится с вероятностью 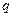 ,то вероятность того, что в
,то вероятность того, что в  испытаниях событие
испытаниях событие  появится ровно
появится ровно 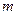 раз рассчитывается по формуле
раз рассчитывается по формуле
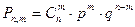
Эта формула целесообразна при небольших  .
.
Теорема (локальная теорема Муавра-Лапласа):
Если вероятность 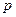 появления события
появления события  в результате каждого из
в результате каждого из  независимых испытаний постоянна и отлична от 0 и 1, то при достаточно больших
независимых испытаний постоянна и отлична от 0 и 1, то при достаточно больших  вероятность того, что в
вероятность того, что в  испытаниях событие
испытаниях событие  появится ровно
появится ровно 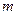 раз имеет представление
раз имеет представление
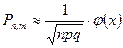 , где
, где 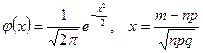 .
.
Функция 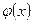 - непрерывная и положительная при любых
- непрерывная и положительная при любых  , четная и
, четная и 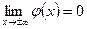 .
.
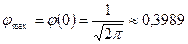 .
.
При 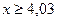 полагают
полагают 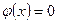 .
.
Закон Пуассона:
Если  достаточно велико,
достаточно велико, 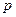 - достаточно мало, то с наименьшей погрешностью
- достаточно мало, то с наименьшей погрешностью
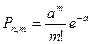 , где
, где 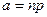 .
.
Интегральная теорема Лапласа:
Если вероятность 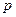 появления события
появления события  в результате каждого из
в результате каждого из  независимых испытаний постоянна и отлична от нуля и единицы, то при достатолчно больших
независимых испытаний постоянна и отлична от нуля и единицы, то при достатолчно больших  вероятность того, что событие
вероятность того, что событие  наступит от
наступит от 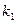 до
до 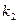 раз имеет слудующее представление
раз имеет слудующее представление 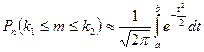 , где
, где 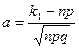 ;
; 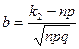 .
.
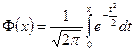 - функция Лапласа.
- функция Лапласа.
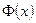 - непрерывна при любых
- непрерывна при любых  , нечетная
, нечетная 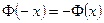 .
.
При 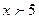 полагают
полагают 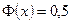 .
.
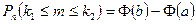 .
.
6.4. Случайные величины:
Определение:
Случайной величиной называется величина, которая в результате ОКУ заведомо принимает одно и только одно из своих возможных числовых значений, причем заранее неизвестно какое именно.
Определение:
Случайная величина, возможные значения которой изолированы друг от друга называется дискретной (ДСВ).
Определение:
Случайная величина, возможные значения которой непрерывно заполняют некоторый интервал, конечный или бесконечный, называется непрерывной (НСВ).
Определение:
Всякое соответствие, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями называется законом распределения случайной величины.
Простейшей формой закона распределения ДСВ является ряд распределения, т.е. таблица, в которой перечислены все возможные значения случайной величины и соответствующие им вероятности, т.е.
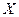 |  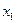 | 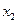 | 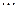 | 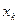 |
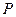 | 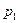 | 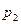 | 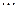 | 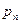 |
Где 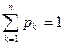
Определение:
Ломаная, соединяющая точки с координатами 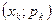 ,
, 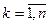 называется многоугольником или полигоном распределения ДСВ.
называется многоугольником или полигоном распределения ДСВ.
Определение:
Возможное значение случайной величины, имеющее наибольшую вероятность, называется модой этой случайной величины.
Определение:
Функцией распределения 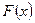 случайной величины
случайной величины 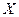 называется вероятность того, что эта случайная величина примет значение меньшее, чем
называется вероятность того, что эта случайная величина примет значение меньшее, чем  , т.е.
, т.е. 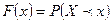 .
.
Основные свойства 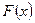 :
:
- значения функции распределения принадлежат отрезку 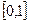 ;
;
- функция распределения неубывающая;
- если 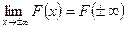 , то
, то 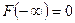 и
и 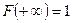 ;
;
- если возможные значения НСВ принадлежат 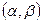 , то при
, то при 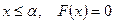 , а при
, а при
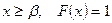 .
.
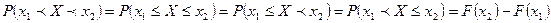 - вероятность попадания НСВ в интервал любого типа.
- вероятность попадания НСВ в интервал любого типа.
Определение:
Предел средней плотности распределения вероятности НСВ в 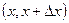 , при условии, что длина этого интервала
, при условии, что длина этого интервала 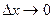 , называется плотностью распределения вероятности данной случайной величины в точке
, называется плотностью распределения вероятности данной случайной величины в точке  .
.
Обозначение: 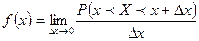 .
.
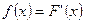 для
для 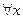 .
.
Теорема:
Вероятность попадания НСВ 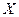 в интервал
в интервал 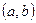 равна определенному интервалу на соответствующем отрезке
равна определенному интервалу на соответствующем отрезке 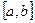 от плотности распределения, т.е.
от плотности распределения, т.е. 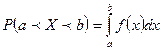 .
.
Связь между функцией распределения и плотностью распределения НСВ:
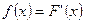 для
для 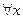 и
и 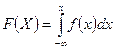 .
.
Свойства плотности распределения:
- 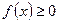 при
при 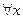 ;
;
- 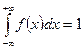 ;
;
6.4. Числовые характеристики случайных величин:
Для дискретной случайной величины
Определение:
Сумма произведений всех возможных значений ДСВ на соответствующие им вероятности называется математическим ожиданием этой случайной величины.
Т.о. 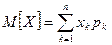 .
.
Математическое ожидание – константа, имеющая размерность случайной величины.
Математическое ожидание приближенно равно среднему арифметическому всех возможных значений данной случайной величины.
Свойства математического ожидания:
- 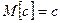 ;
;
- 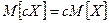 ;
;
- 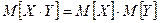 для независимых ДСВ;
для независимых ДСВ;
- 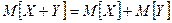 для независимых ДСВ;
для независимых ДСВ;
- 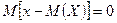 .
.
Для непрерывной случайной величины
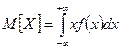 .
.
Вероятностный смысл и свойства ДСВ остаются справедливыми.
2 ) Дисперия
Определение:
Математическое ожидание квадрата отклонения случайной величины от своего математического ожидания называется дисперсией.
Т.о 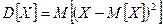 или
или 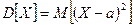 .
.
Дисперсия – константа, имеющая размерность квадрата случай величины.
Дисперсия характеризует степень разброса возможных значений случайной величины относительно ее центра, т.е. МО.
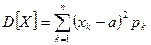 - для ДСВ.
- для ДСВ.
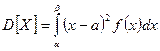 - для НСВ.
- для НСВ.
Теорема: 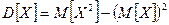 .
.
Свойства дисперсии:
- 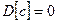 ;
;
- 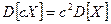 ;
;
- 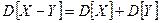 для независимых ДСВ;
для независимых ДСВ;
- 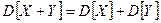 для независимых ДСВ.
для независимых ДСВ.
3) Среднее квадратическое отклонение:
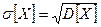 .
.
СКО имеет размерность СВ, вероятностный смысл тот же, что и у 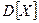 .
.
Теорема:
Если проводится  независимых испытаний, в результате каждого из которых событие
независимых испытаний, в результате каждого из которых событие  может появится в вероятностью
может появится в вероятностью 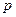 и не появится с вероятностью
и не появится с вероятностью 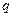 , то
, то 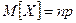 ,
, 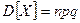 .
.

 2015-06-26
2015-06-26 1440
1440








