5.1. Основные понятия:
Пусть 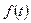 - действительная функция действительной переменной
- действительная функция действительной переменной 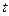 , которая рассматривается как время.
, которая рассматривается как время.
Определение:
Функция 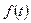 называется оригиналом, если она удовлетворяет трем условиям
называется оригиналом, если она удовлетворяет трем условиям
-
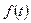 при
при 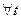 непрерывна или имеет конечное число точек разрыва первого рода;
непрерывна или имеет конечное число точек разрыва первого рода; -
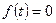 при
при 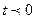 ;
; - существуют такие действительные числа
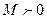 и
и 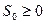 , что при
, что при 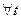
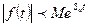 , где
, где 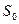 - называется показателем роста оригинала.
- называется показателем роста оригинала.
Определение:
Изображением оригинала 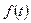 называется функция
называется функция 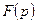 комплексной переменной
комплексной переменной 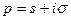 , определяемая равенством
, определяемая равенством 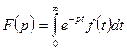 .
.
Символическая запись перехода от ориганала 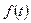 к изображению
к изображению 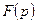 :
: 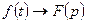 .
.
5.2. Свойства преобразований Лапласа:
1) Если 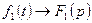 и
и 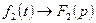 , то
, то 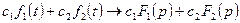 - свойство линейности;
- свойство линейности;
2) Если 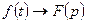 и действительное число
и действительное число 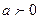 , то
, то 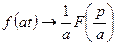 - свойство подобия;
- свойство подобия;
3) Если 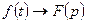 и действительное число
и действительное число 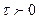 , то
, то 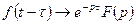 - свойство запаздывания или сдвига;
- свойство запаздывания или сдвига;
4) Если 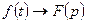 , то
, то 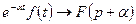 - свойство смещения или затухания;
- свойство смещения или затухания;
5) Если 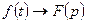 и
и 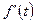 является оригиналом, то
является оригиналом, то 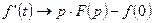 - свойство дифференцирования оригинала;
- свойство дифференцирования оригинала;
Следствие:
Если 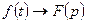 и
и 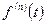 является оригиналом, то
является оригиналом, то
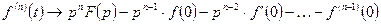 , где
, где 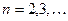
6) Если 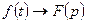 , то
, то 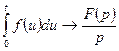 - свойство интегрирования оригинала;
- свойство интегрирования оригинала;
7) Если 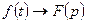 , то
, то 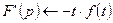 - свойство дифференцирования изображения;
- свойство дифференцирования изображения;
8) Если 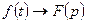 , то
, то 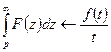
5.3. Свертка функций:
Определение:
Сверткой двух функций 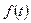 и
и 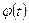 называется функция
называется функция 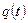 , определяемая равенством
, определяемая равенством
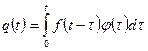 .
.
Обозначение: 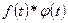 .
.
Теорема умножения изображений:
Если 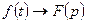 ,
, 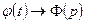 , то
, то 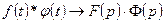 , т.е. если изображения перемножаются, то их оригиналы свертываются.
, т.е. если изображения перемножаются, то их оригиналы свертываются.
Формула обращения:
Если функция 
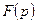 является изображением некоторого оригинала
является изображением некоторого оригинала 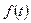 , то в каждой точке непрерывности оригинала справедлива формула
, то в каждой точке непрерывности оригинала справедлива формула 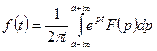 .
.
5.4. Теоремы разложения:
Теорема 1:
Если изображение 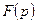 не конечного круга, т.е. при
не конечного круга, т.е. при 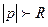 представлено рядом Лорана вида
представлено рядом Лорана вида 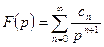 , то соответствующий оригинал является суммой степенного ряда
, то соответствующий оригинал является суммой степенного ряда 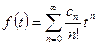 , где
, где 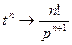 , который сходится при всех
, который сходится при всех 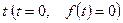 .
.
Теорема 2:
Если изображение представлено правильной рациональной дробью 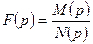 со знаменателем, имеющем только простые корни, то соответствующий оригинал находят по формуле
со знаменателем, имеющем только простые корни, то соответствующий оригинал находят по формуле 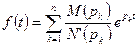 .
.
Теорема 3:
Если изображение представлено правильной рациональной дробью 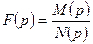 со знаменателем, имеющем кратные корни
со знаменателем, имеющем кратные корни 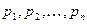 , то соответствующий оригинал находят по формуле
, то соответствующий оригинал находят по формуле 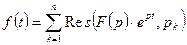 .
.
5.5 Таблица оригиналов и изображений:
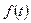 - оригинал - оригинал
| 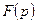 - изображение - изображение
| |
| 1. | 1 
| 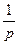
|
| 2. | 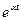
| 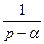
|
| 3. | 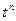
| 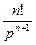
|
| 4. | 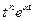
| 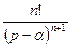
|
| 5. | 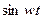
| 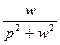
|
| 6. | 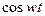
| 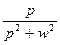
|
| 7. | 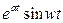
| 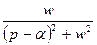
|
| 8. | 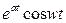
| 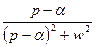
|
| 9. | 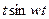
| 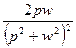
|
| 10. | 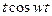
| 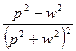
|
| 11. | 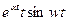
| 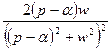
|
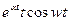
| 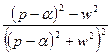
| |
| 13. | 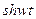
| 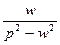
|
| 14. | 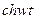
| 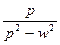
|
| 15. | 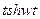
| 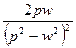
|
| 16. | 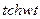
| 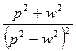
|
| 17. | 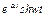
| 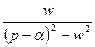
|
| 18. | 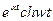
| 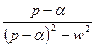
|
| 19. | 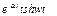
| 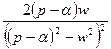
|
| 20. | 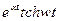
| 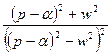
|
| 21. | 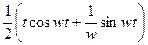
| 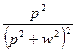
|
| 22. | 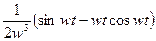
| 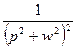
|
 2015-06-26
2015-06-26 304
304








