3. Теорема Коши (для односвязной области):
Если функция  аналитическая в каждой точке области
аналитическая в каждой точке области 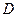 и на ее границе
и на ее границе 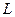 , то
, то 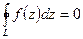 .
.
Теорема Коши (для многосвязной области):
Если функция  аналитическая в многосвязной области
аналитическая в многосвязной области 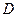 , границей которой служат кривые
, границей которой служат кривые 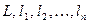 , то
, то 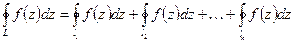 (все границы области обходятся в одном направлении)
(все границы области обходятся в одном направлении)
4. 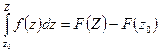 ;
;
5. Контурный интеграл от аналитической функции не зависит от формы кривой интегрирования, но зависит от начальной 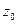 и конечной
и конечной 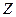 точек пути, т.е.
точек пути, т.е. 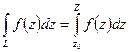 .
.
6. Используя интегральную формулу Коши, имеем:
· 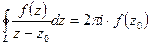 , где
, где  - аналитическая в односвязной области
- аналитическая в односвязной области 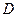 и на ее границе
и на ее границе 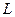
· 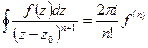 , где
, где  - аналитическая
- аналитическая
7. 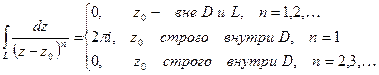
8. Теорема:
Если функция  аналитическая в каждой точке области
аналитическая в каждой точке области 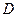 , ограниченной контуром
, ограниченной контуром 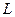 , за исключением конечного числа изолированных особых точек
, за исключением конечного числа изолированных особых точек 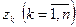 , лежащих строго внутри области
, лежащих строго внутри области 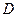 , то справедливо равентство:
, то справедливо равентство:
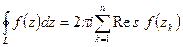 .
.
4.5. Ряды Тейлора и Лорана:
Определение:
Степенной ряд 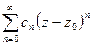 , коэффициенты которого рассчитываются по формулам
, коэффициенты которого рассчитываются по формулам
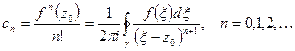 называется рядом Тейлора функции
называется рядом Тейлора функции  , где
, где 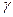 - произвольный замкнутый контур, содержащий строго внутри точку
- произвольный замкнутый контур, содержащий строго внутри точку 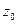 .
.
Определение:
Функциональный ряд вида 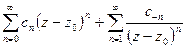 , где
, где
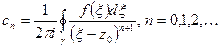 и
и 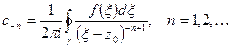
называется рядом Лорана функции  или компактная форма
или компактная форма
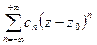 , где
, где 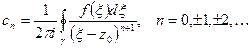
Ряд Лорана состоит из двух частей:
-
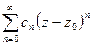 - правильная
- правильная
-
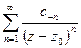 - главная часть.
- главная часть.
4.6. Типы особых точек:
Определение:
Точка 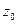 называется
называется 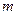 - кратным нулем функции
- кратным нулем функции  , если в разложении Тейлора этой функции в окрестности т.
, если в разложении Тейлора этой функции в окрестности т. 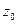
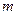 первых коэффициентов равны нулю:
первых коэффициентов равны нулю: 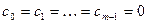 , но
, но 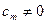 .
.
Определение:
Особая точка 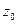 называется изолированной, если существует достаточно малая окрестность этой точки, не содержащая других особых точек данной функции.
называется изолированной, если существует достаточно малая окрестность этой точки, не содержащая других особых точек данной функции.
Определение:
Точка 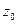 называется особой точкой функции
называется особой точкой функции  , если в этой точке функция не аналитическая.
, если в этой точке функция не аналитическая.
Определение:
Точка 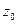 называется устранимой особой точкой
называется устранимой особой точкой  , если разложение Лорана этой функции в окрестности этой точки не содержит отрицательных степеней
, если разложение Лорана этой функции в окрестности этой точки не содержит отрицательных степеней 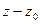 , т.е.
, т.е.
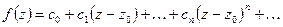
Определение:
Точка 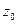 называется полюсом
называется полюсом  , если разложение Лорана этой функции имеет конечное число отрицательных степеней, т.е.
, если разложение Лорана этой функции имеет конечное число отрицательных степеней, т.е.
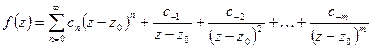 .
.
Если 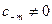 , то
, то 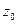 -
- 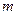 кратный полюс, если
кратный полюс, если 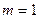 , то простой.
, то простой.
Определение:
Точка 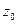 называется существенно особой точкой
называется существенно особой точкой  , если разложение Лорана этой функции содержит бесчисленное множество отрицательных степеней
, если разложение Лорана этой функции содержит бесчисленное множество отрицательных степеней 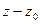 , т.е.
, т.е.
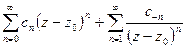 .
.
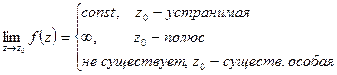
Теорема:
- 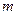 - кратный нуль функции
- кратный нуль функции 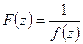 является
является 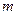 - кратным полюсом функции
- кратным полюсом функции  ;
;
- 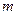 - кратный полюс функции
- кратный полюс функции  является
является 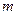 - кратным нулем функции
- кратным нулем функции 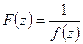 .
.
Алгоритм определения типа особой точки:
- Применить теорему о связи между нулями и полюсами функций;
или
- Вычислить
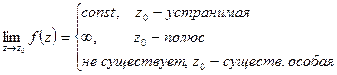 ;
;
или
- Воспользоваться определением.
4.7. Вычеты:
Определение:
Число 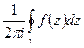 называется вычетом функции
называется вычетом функции  относительно изолированной точки
относительно изолированной точки 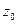 .
.
Обозначение: 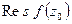 =
= 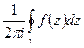 .
.
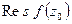 =
= 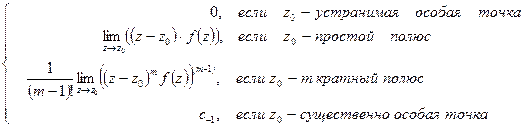
 2015-06-26
2015-06-26 293
293








