Ранее было отмечено, что классическое определение вероятности применимо только для тех событий, которые могут появиться в результате испытаний, обладающих симметрией возможных исходов, т.е. сводящихся к схеме случаев. Но существует большой класс событий, вероятности которых не могут быть вычислены с помощью классического определения. В первую очередь это события, которые не являются равновозможными исходами испытаний. Например, при бросании неправильной игральной кости выпадение различных граней не является равновозможным. Или, если монета сплющена, то, очевидно, что события «появление герба» и «появление решки» нельзя считать равновозможными. Таким образом, формула (1) для расчёта вероятности любого из них окажется неприемлема.
В таких случаях используется статистическое определение вероятности.
Опр. Статистической вероятностью события 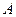 называется относительная частота (частость) появления этого события в n произведённых испытаниях, то есть,
называется относительная частота (частость) появления этого события в n произведённых испытаниях, то есть, 
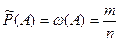 , (2)
, (2)
где
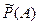 - статистическая вероятность события
- статистическая вероятность события 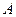 ;
;
|
|
|
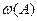 - относительная частота (частость) события
- относительная частота (частость) события 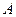 ;
;
m – число испытаний, в которых появилось событие 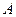 ;
;
n – общее число испытаний.
В отличие от «математической» вероятности 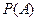 , рассматриваемой в классическом определении, статистическая вероятность
, рассматриваемой в классическом определении, статистическая вероятность 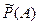 является характеристикой опытной, экспериментальной. Если
является характеристикой опытной, экспериментальной. Если 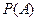 есть доля случаев, благоприятствующих событию
есть доля случаев, благоприятствующих событию 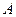 , которая определяется непосредственно, без каких-либо испытаний, то
, которая определяется непосредственно, без каких-либо испытаний, то 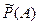 есть доля тех фактически произведённых испытаний, в которых событие
есть доля тех фактически произведённых испытаний, в которых событие 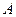 появилось.
появилось.
Статистическое определение вероятности, как и понятия и методы теории вероятностей в целом, применимы не к любым событиям с неопределённым исходом, которые в житейской практике считаются случайными, а только к тем из них, которые обладают определёнными свойствами.
1. Рассматриваемые события должны быть исходами только тех испытаний, которые могут быть воспроизведены неограниченное число раз при одном и том же комплексе условий.
2. События должны обладать так называемой статистической устойчивостью, или устойчивостью относительных частот, т.е. в различных сериях испытаний относительная частота (частость) события изменяется незначительно (тем меньше, чем больше число испытаний), колеблясь около постоянного числа. Причём, этим постоянным числом является вероятность события.
Факт приближения относительной частоты, или частости события к его вероятности при увеличении числа испытаний, сводящихся к схеме случаев, подтверждается многочисленными массовыми экспериментами.
3. Число испытаний, в результате которых появляется событие А, должно быть достаточно велико, т.к. только в этом случае можно считать вероятность события 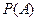 приближённо равной её относительной частоте.
приближённо равной её относительной частоте.
|
|
|
Пример 3. Было проведено 10 серий бросания монеты, по 1000 бросаний в каждой. Относительные частоты выпадения герба оказались равными 0,501; 0,485; 0,509; 0,536; 0,485; 0,488; 0,500; 0,497; 0,494; 0,484. Все эти частоты группируются около числа 0,5.
Рассмотрим ещё один пример с бросанием монеты.
Пример 4. Данные результатов бросания монеты приведены в таблице 1.
Таблица 1. Результаты выпадения герба при бросании монеты.
| Экспериментатор | Число бросаний | Число выпадений герба | Относительная частота |
| Бюффон | 4 040 | 2 048 | 0,5069 |
| К. Пирсон | 12 000 | 6 019 | 0,5016 |
| К. Пирсон | 24 000 | 12 012 | 0,5005 |
Здесь относительные частоты незначительно отклоняются от числа 0,5, причём тем меньше, чем больше испытаний. При 4 040 испытаниях отклонение равно 0,0069, а при 24 000 – 0,0005.
 2015-06-26
2015-06-26 2376
2376
