Пусть события 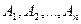 независимы в совокупности, причем
независимы в совокупности, причем 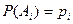 , где
, где 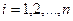 .
.
Теорема 5. Вероятность наступления события 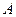 , состоящего в появлении хотя бы одного из событий
, состоящего в появлении хотя бы одного из событий 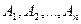 независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий 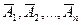 :
:
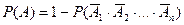
или
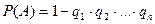 , (15)
, (15)
где 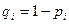 ,
, 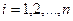 .
.
В частности, если все 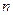 событий имеют одинаковую вероятность, равную
событий имеют одинаковую вероятность, равную 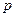 , т.е.
, т.е. 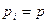 , где
, где 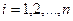 , вероятность появления, хотя бы одного из этих событий равна
, вероятность появления, хотя бы одного из этих событий равна
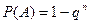 . (16)
. (16)
Пример 8. Вероятность хотя бы одного попадания стрелком в мишень при трех выстрелах равна 0,875. Найдите вероятность попадания при одном выстреле.
Решение.
Вероятность попадания в мишень хотя бы при одном из трех выстрелов (событие 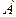 ) равна
) равна 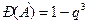 , где
, где 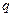 - вероятность промаха.
- вероятность промаха.
По условию 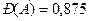 , тогда
, тогда 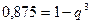 или
или 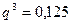 , отсюда
, отсюда 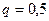 .
.
Тогда искомая вероятность 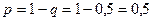 .
.
Ответ: 0,5. [2, с.35-37]
 2015-06-26
2015-06-26 556
556








