Методы санитарной статистики
МЕТОДЫ САНИТАРНОЙ СТАТИСТИКИ
Профессор В.Н.Филатов
заведующий кафедрой социальной гигиены, экономики и управления здравоохранением
ГОУ ДПО СПбМАПО Росздрава»,
главный специалист по вопросам экономики и управления здравоохранением
Комитета по здравоохранению Санкт–Петербурга
Доцент А.Т.Бойко
кафедра социальной гигиены, экономики и управления здравоохранением ГОУ ДПО СПбМАПО Росздрава»,
- Относительные и средние величины
- Оценка значимости различия выборочных относительных и средних величин
- Статистические методы изучения связи
- Метод стандартизации
- Методы анализа динамики явлений
- Выявление групп риска. Относительный и абсолютный риски
- Изучение многомерных зависимостей
ОТНОСИТЕЛЬНЫЕ И СРЕДНИЕ ВЕЛИЧИНЫ.
Относительные величины. В ходе статистической сводки информации, полученной в результате наблюдения или из отчетных документов, характеристики медицинских или санитарно-гигиенических явлений оказываются представлены в абсолютных величинах. В ряде случаев именно оценка их абсолютной величины представляет специальный интерес. Так, важно знать абсолютное число заболеваний редкой инфекционной болезнью, например, инфекцией, близкой к ликвидации, или инфекцией, которая ранее считалась ликвидированной. Однако абсолютные величины недостаточно пригодны для целей анализа, сравнения двух явлений, оценки динамики явления по временным периодам, связи между явлениями и т.п. В большинстве случаев они являются основой для расчета относительных величин или коэффициентов.
Наиболее часто в практике врача-гигиениста используют следующие виды относительных величин:
1. Относительные величины частоты (показатели уровня, интенсивные показатели).
2. Относительные величины распределения (показатели структуры, экстенсивные показатели).
3. Относительные величины наглядности.
4. Относительные величины соотношения.
5. Относительные величины динамики.
Относительные величины частоты используются в тех случаях, когда необходимо оценить распространенность изучаемого явления в среде, с которой оно связано. Иными словами, относительные величины частоты отвечают на вопрос как часто встречается изучаемое явление в той среде, в которой оно происходит.
Относительные величины частоты можно рассчитывать к различным основаниям (k). В санитарной статистике при вычислении уровней рождаемости, смертности, естественного прироста населения, общей заболеваемости и т.п. за основание обычно принимают k = 1 000 человек населения; вычисление показателей смертности или заболеваемости в отношении какой-либо отдельной болезни или группы болезней производится на 10 000 или на 100 000 населения; вычисление показателей временной нетрудоспособности (число больных лиц, случаев и дней) в связи с заболеваниями производится на 100 работающих. Соответственно коэффициент интенсивности выражается в промилле (0/00), продецимилле (0/000), просантимилле (0/0000) или в процентах (0/0). Вычисления относительных величин частоты осуществляется по формуле:
абсолютная величина явления
относительная величина = * k (5)
частоты абсолютная величина среды
Если коэффициенты вычисляются за период времени меньше года, в целях сопоставимости их надо привести к годичному уровню, т.е. установить, чему бы равнялся коэффициент, если бы частота измеряемого явления в течение года была такой, как в период наблюдения. Для этого в приведенной выше формуле числитель умножается на 12 (число месяцев в году), а знаменатель - на число месяцев наблюдения.
Относительные величины распределения используются в тех случаях, когда необходимо количественно характеризовать распределение целого на составляющие его части. Иными словами, относительные величины распределения отвечают на вопрос о том, какую долю (%) среди всего явления в целом, принимаемого за 100%, составляет его любая составная часть. Необходимо отметить, что при вычислении относительных величин распределения могут быть получены либо полная структура анализируемого явления, когда сумма относительных величин составляет 100%, либо относительные доли, характеризующие отношение отдельных частей явления к целому.
Определение относительных величин распределения осуществляется по формуле:
| относительная величина распределения явления | = | абсолютная величина любой составной части явления х 100 % абсолютная величина всего изучаемого явления | (6) |
Относительные величины распределения используются для характеристики структуры заболеваемости по нозологическим формам, структуры смертности, летальности, потерь трудоспособности. Кроме того, эти показатели используют при анализе структуры больных по срокам обращения за медицинской помощью, срокам изоляции и госпитализации и т.п.
Относительные величины наглядности применяют в тех случаях, когда необходимо в наглядном виде сопоставить несколько однородных абсолютных или производных (относительных и средних) величин. Методика вычисления относительных величин наглядности заключается в том, что одна из сравниваемых величин принимается за 100%, а остальные величины с помощью обычной пропорции пересчитываются в показателях по отношению к этому числу.
Относительные величины соотношения используются в тех случаях, когда необходимо сопоставлять изучаемое явление не связанное со средой, т.е. оценить соотношение независимых друг от друга явления и среды, объединенных между собой только логически, по смыслу. Примером применения относительных величин соотношения могут служить показатели обеспеченности населения страны (региона, административной территории) врачами, больничными койками; показатели оперируемости; показатели охвата лечившихся больных специальными диагностическими исследованиями, лабораторными исследованиями и др. Методика расчета относительных величин соотношения аналогична методике расчета относительных величин частоты.
Относительные величины динамики применяются при анализе рядов абсолютных, относительных или средних величин, отражающих изменения явления во времени (подробнее см. 3.5.5).
Средние величины. Кроме относительных величин (коэффициентов) статистические совокупности могут быть охарактеризованы с помощью средних величин. Средняя величина-это сводная обобщающая характеристика совокупности наблюдений по какому-либо количественно выраженному признаку. Иными словами, средняя величина отражает одним числом ряд индивидуальных варьирующих (колеблющихся) наблюдений. Необходимым условием научного применения средних величин является качественная однородность изучаемой совокупности по основным, определяющим признакам.
Средние величины используются при изучении физического развития населения, закономерностей течения различных процессов в здоровом и больном организме, для оценки эффективности лекарственных препаратов и решения целого ряда других задач. Из различных видов средних величин наиболее часто употребляются:
· средняя арифметическая (простая и взвешенная);
· медиана и мода;
· средняя геометрическая;
· средняя хронологическая (см. анализ рядов динамики).
Средняя арифметическая (`x) простая применяется в том случае, если число наблюдений (n) небольшое (n<30) и значения вариант (варьирующего признака) обычно не повторяются. Методика расчета следующая:
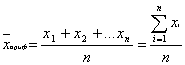 (7)
(7)
где
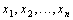 - значения варьирующего признака;
- значения варьирующего признака;
n - число наблюдений;
å -знак суммирования.
(Здесь и далее суммирование проводится в интервале от i = 1 до n, если иное не оговорено).
Пример. Определить среднюю арифметическую запыленности атмосферного воздуха города, если в 5 точках получены следующие данные о концентрации пыли (мг/м3): 0.085; 0.105; 0.125; 0.145; 0.163.
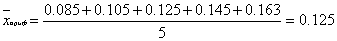 мг/м3
мг/м3
При большом числе наблюдений удобнее пользоваться средней арифметической взвешенной, которую рассчитывают на сгруппированных вариационных рядах, методика построения которых опубликована [20]. Формула для расчета средней арифметической взвешенной имеет вид:
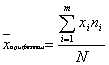
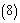
где
xi - середины интервалов для сгруппированного ряда;
ni - число наблюдений в каждом интервале;
N - общее число наблюдений, 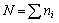 ;
;
m - число классов (групп) в интервальном ряду.
Средняя величина не характеризует изучаемые явления с точки зрения индивидуальных колебаний значений признака, что в свою очередь, не позволяет решить вопрос, насколько типичной является полученная средняя величина. Это можно сделать только с помощью среднего квадратического отклонения (s), вычисляемого по формуле:
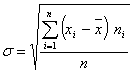 (9)
(9)
При числе наблюдений n < 30 знаменатель данной формулы принимает вид (n – 1).
Среднее квадратическое отклонение служит для:
а) измерения колебания значений вариационного ряда;
б) сравнительной оценки степени соответствия средних арифметических величин тем вариационным рядам для которых они вычислены;
в) индивидуальной оценки отдельных членов группы внутри совокупности (сигмальная оценка) и ориентировочных расчетов распределения членов группы вокруг средней арифметической;
г) оценки достоверности различий двух средних величин.
Так как среднее квадратическое отклонение является именованной величиной, то сравнивать колеблемость двух средних величин, выраженных в различных единицах измерения, по абсолютным размерам средних квадратических отклонений (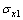 ,
, 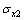 ) невозможно. В таких случаях следует использовать коэффициент вариации, выраженный в процентах:
) невозможно. В таких случаях следует использовать коэффициент вариации, выраженный в процентах:
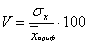 (10)
(10)
При этом, чем больше коэффициент вариации, тем больше размах вариационного ряда от средних значений.
Мода (Mo) - это та варианта, которая встречается в вариационном ряду наиболее часто. В санитарной статистике она может быть использована для оценки средней длительности заболевания, особенно при малом количестве больных данной болезнью; при резко выраженной асимметрии ряда; при отсутствии достаточных сведений о характере распределения исследуемых величин, при изучении полуколичественных и качественных признаков.
Медиана (Me) - варианта, которая находится в середине ранжированного ряда распределения и, следовательно, делит его на две равные части. При нечетном числе членов ранжированного ряда центральная варианта и будет его медианой. При четном числе членов ряда медиана определяется как полусумма двух соседних вариант, расположенных в центре ряда. Медианой можно пользоваться как ориентировочной средней, если не представляется возможным определить среднюю арифметическую. В отличие от средней арифметической на размер моды и медианы значения крайних вариант, имеющихся в вариационном ряду, не влияют.
Между средней арифметической (`x), медианой (Me) и модой (Mo) существуют определенные соотношения, позволяющие определить каждую из этих величин, если известны числовые значения двух других. Соотношение эти следующие:
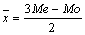 (11)
(11)
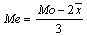 (12)
(12)
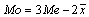 (13)
(13)
Средняя геометрическая применяется в тех случаях, когда ряд варьирующих величин отражает изменение признака в геометрической прогрессии. Формула для ее расчета имеет вид:
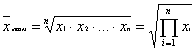 (14)
(14)
где
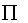 - произведение вариант ряда;
- произведение вариант ряда;
xi - отдельные варианты ряда;
n - число вариант.
Обычно среднюю геометрическую вычисляют с помощью десятичных, натуральных или двоичных логарифмов [20].
Оценка достоверности статистических показателей. Статистические показатели и характеристики медицинских и санитарно-гигиенических явлений получаемые в практике, представляют собой результаты наблюдения ограниченного числа этих явлений. Теоретически же возможное число этих состояний бесконечно. Поэтому, в силу выборочного характера наблюдений, наши заключения о закономерностях, наблюдаемых в изучаемых явлениях, сопряжены с определенным риском принятия ошибочных гипотез. Степень такого риска определяется ошибками репрезентативности используемых показателей и характеристик.
Средняя квадратическая ошибка средней арифметической величины (m`x) вычисляется по формуле:
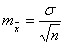 (16)
(16)
где
s - среднее квадратическое отклонение средней арифметической величины;
n - число наблюдений.
Ошибки выборочной относительной величины (P) вычисляются:
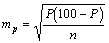 (17)
(17)
или
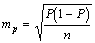 (18)
(18)
где
P - выборочная относительная величина (в % или долях единицы соответственно);
n - число наблюдений.
Теоретически установлено, что в случае нормального (или близкого к нормальному) распределения вариант, генеральная средняя находится в пределах:
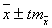 и
и 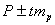 (19)
(19)
где
t - доверительный коэффициент.
В зависимости от значения коэффициента, генеральная величина будет находится в пределах:
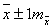 и
и 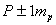 - c вероятностью 68,3%;
- c вероятностью 68,3%;
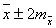 и
и 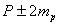 - с вероятностью 95,4%;
- с вероятностью 95,4%;
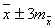 и
и 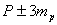 - с вероятностью 99,7%.
- с вероятностью 99,7%.
В санитарно-гигиенических и медицинских исследованиях минимально приемлемым уровнем доверительной вероятности (надежности) выборочных показателей считается 95.4% (t = 2), т.е. доверительный интервал принимается
и.
 2015-05-20
2015-05-20 4604
4604