В приложениях теории вероятностей часто встречается некоторая стандартная схема, называемая схемой независимых испытаний или схемой Бернулли. Имеет место теорема.
Теорема. Если вероятность 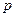 наступления событии А в каждом испытании постоянна, то вероятность
наступления событии А в каждом испытании постоянна, то вероятность 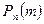 того, что событие А наступит т раз в
того, что событие А наступит т раз в 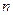 независимых испытания, равна
независимых испытания, равна
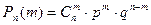 , (19)
, (19)
или
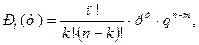 (19*)
(19*)
где 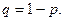
Вероятность того, что событие наступит: а) менее 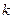 раз; б) более
раз; б) более 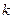 раз; в) не менее
раз; в) не менее 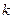 раз; г) не более
раз; г) не более 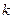 раз – находят соответственно по формулам:
раз – находят соответственно по формулам:
а) 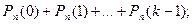
б) 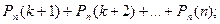
в) 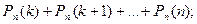
г) 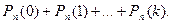 (20)
(20)
Опр. Число 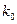 , которому при заданном
, которому при заданном 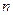 соответствует максимальная биномиальная вероятность
соответствует максимальная биномиальная вероятность 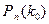 , называется наивероятнейшим.
, называется наивероятнейшим.
Для нахождения наивероятнейшего числа 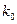 по заданным
по заданным 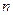 и р можно воспользоваться неравенствами
и р можно воспользоваться неравенствами
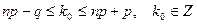 , (21)
, (21)
причем:
а) если число 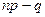 - дробное, то существует одно наивероятнейшее число
- дробное, то существует одно наивероятнейшее число 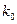 ;
;
б) если число 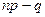 - целое, то существует два наивероятнейших числа:
- целое, то существует два наивероятнейших числа: 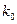 и
и 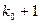 ;
;
в) если число 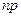 - целое, то наивероятнейшее число
- целое, то наивероятнейшее число 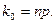
*Пусть производится 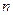 независимых опытов, каждый из которых имеет т
независимых опытов, каждый из которых имеет т 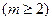 попарно несовместных и единственно возможных сходов
попарно несовместных и единственно возможных сходов 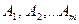 с вероятностями
с вероятностями 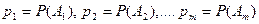 , одинаковыми во всех опытах (
, одинаковыми во всех опытах (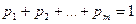 ). Для произвольных целых неотрицательных чисел
). Для произвольных целых неотрицательных чисел 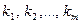
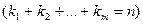 обозначим через
обозначим через 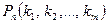 вероятность того, что в
вероятность того, что в 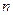 опытах исход
опытах исход 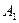 наступит
наступит 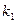 раз, исход
раз, исход 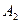 наступит
наступит 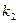 раз и т.д., исход
раз и т.д., исход 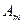 наступит
наступит 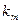 раз. Тогда справедлива формула
раз. Тогда справедлива формула
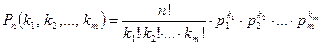 , (22)
, (22)
которая является обобщением формулы Бернулли на случай, когда каждый из независимых опытов 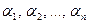 имеет т исходов
имеет т исходов 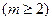 .
.
Пример 10. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть: две партии из четырех или три партии из шести (ничьи во внимание не принимаются)?
Решение.
Так как играют равносильные шахматисты, то вероятность выигрыша 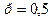 , следовательно, вероятность проигрыша
, следовательно, вероятность проигрыша 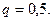
Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли.
Найдем вероятность того, что две партии из четырех будут выиграны. Воспользуемся формулой 19*:
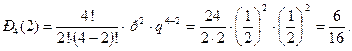
Найдем вероятность того, что три партии из шести будут выиграны:
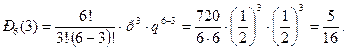
Так как 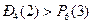 , то вероятнее выиграть две партии из четырех, чем три из шести.
, то вероятнее выиграть две партии из четырех, чем три из шести.
Ответ: вероятнее выиграть две партии из четырех. [2, с.46-47]
Пример 11. Товаровед осматривает 24 образца товаров. Вероятность того, что каждый из образцов будет признан годным к продаже, равна 0,6. Найдите наивероятнейшее число образцов, которые товаровед признает годными к продаже.
Решение.
По условию 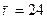 ,
, 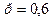 ,
, 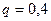 . Воспользуемся неравенством 21:
. Воспользуемся неравенством 21:
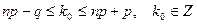 .
.
Подставляя данные задачи, получим
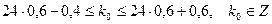
или
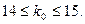
Так как 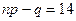 - целое число, то наивероятнейших чисел два:
- целое число, то наивероятнейших чисел два: 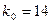 и
и 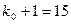 .
.
Ответ: 14; 15. [2, с.58-59]
 2015-06-26
2015-06-26 3914
3914








