Теоретическое обоснование. Резонанс напряжений в последовательном колебательном контуре

Резонанс напряжений в последовательном колебательном контуре.

1. Цель работы: Изучение и экспериментальное исследование резонанса в цепи с последовательным соединением активного сопротивления, катушки индуктивности и конденсатора.

2. Оборудование. Рабочее место в компьютерном классе.

Теоретическое обоснование.

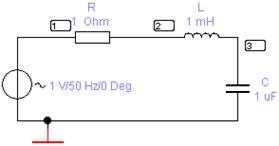Схема последовательного резонансного контура состоящего из последовательно соединенных элементов R, L, С представлена на рис. 1. Полное входное сопротивление цепи может быть определено по формуле:

Z = R + jX = R + j(X_L – X_C) = R + j(ωL – 1/(ωC)),

где R – активное сопротивление цепи;

X=(ωL –1/(ωC)) - реактивное сопротивление цепи; ωL–реактивное индуктивное сопротивление цепи;

1/(ωC - реактивное емкостное сопротивление цепи; 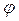=arctg(X/R) - фазовый сдвиг между входным напряжением и током в цепи;

рис. 1. ω = 2πf – круговая частота; f – частота тока и напряжения в цепи.

При изменении частоты от 0 до ∞ реактивная составляющая сопротивления контура изменяется от –∞ до +∞. На частоте ω_о реактивное сопротивление контура равно нулю: ωL – 1/(ωC = 0. Частота ω_о = 1 / √ LC называется резонансной частотой.

На этой частоте индуктивное сопротивление контура компенсирует емкостное сопротивление, поэтому полное сопротивление цепи становится равным активной составляющей R.

На резонансной частоте 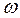₀: I₀ = U/R; U_R0 = U; U_L0 = U_C0 = I_{0 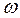0}L = I₀/(ω₀C) =

=U/R* 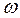L =U/(Rω₀C) = U/R* 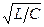= Uρ/R = UQ, где 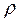= = 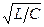ω_oL = 1/(ω_oC) - волновое или характеристическое сопротивление контура, которое равно реактивному сопротивлению индуктивности или емкости контура на резонансной частоте.

Величина Q = ρ / R = ω_оL / R = 1/(ω_оRC) =U_L0/U = U_C0/U - добротность резонансного контура, равная отношению характеристического сопротивления контура к активному сопротивлению. Величина d = 1/Q называется затуханием контура. На резонансной частоте напряжения на L и C равны по значению и противоположны по фазе, поэтому взаимно компенсируются. Наибольший ток в контуре наблюдается на резонансной частоте. Обычно используют контуры с большой добротностью Q >> 1.

На резонансной частоте ω = ω_омаксимум амплитудно-частотной характеристики равен добротности контура (амплитуда напряжения на конденсаторе в Q раз больше амплитуды входного напряжения). Поэтому резонанс в последовательном контуре называют также резонансом напряжений. Полоса пропускания контура определяется частотами ω₁ (f₁)и ω₂ (f₂)между которыми К_U (ω) = Q / √ 2 = 0,707 Q, где К_U (ω) –коэффициент передачи по напряжению.

Полоса пропускания контура при резонансе равна П = ω_о /Q.

В проводимом в работе эксперименте П = f₂ - f₁.

Полоса пропускания контура прямо пропорциональна резонансной частоте и обратно

пропорциональна добротности. При резонансе X_L = 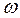L =1/(ωC = X_C, 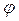= 0. Добиться этого ра­венства можно изменением одной из трех величин 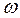, С или L: 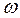₀ = 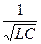; L₀ = 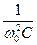; C₀ = 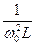.Ток и напряжения на R, L, С при любой частоте 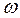, отличной от частоты 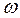₀: I = U/Z; U_R = IR; U_L = I 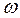L; U_C = I/(ωC

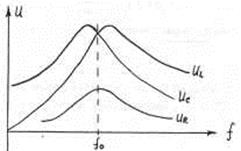При рас­смотрении резонанса напряжений изучаются частот­ные зависимости: I(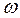), U_L(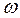), U_C(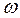), 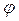(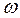), которые приведенына рис.2.

Рис.2. Резонансные характеристики.

При изменении частоты от 0 до 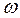₀ реактивное сопро­тивление цепи X имеет емкостной характер и изменяется от - 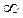до 0, а угол сдвига фаз 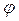от - 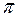/2, до 0. При изменении частоты от 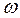₀ до 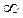X изменяется от 0 до 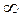, угол 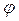от 0 до + 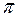/2.