Методы решения задач статической оптимизации

Задачи оптимизации встречаются во многих видах деятельности человека. Особое значение они имеют в технике и экономике. На теоретической базе решения оптимальных задач создаются АСУ П и ТП, локальные оптимальные и адаптивные системы управления машинами, механизмами и устройствами.

Различают задачи статической и динамической оптимизации. В задачах статической оптимизации уравнения движения модели ТП и уравнения цели являются алгебраическими, в задачах динамической оптимизации уравнения движения модели представляются системой дифференциальных уравнений, а уравнения цели (или критерий оптимальности) является интегральным функционалом.

Таким образом, методы решения задач статической оптимизации относятся к разделу поиска экстремума функций (экстремальные задачи), а методы решения задач динамической оптимизации относятся к разделу поиска экстремума функционалов (оптимальные задачи).

Методы статической оптимизации. Решение экстремальных задач.

Классификация экстремальных задач

Останавливаться на задаче поиска экстремума функции одной переменной не будем, т.к. эта задача является частным случаем задачи поиска экстремума функции многих переменных (ФМП). В общем случае можно выделить 2 задачи:

Задача 1: Найти минимум (или максимум, будем говорить о минимизации, т.к. задачу поиска максимума можно получить из задачи на поиск минимума сменой знака) ФМП на открытом множестве М.

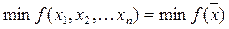, где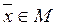

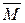
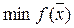Задача 2: Найти минимум ФМП на замкнутом множестве

, где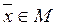

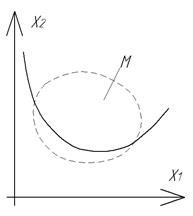Т.е. при 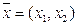и замкнутом множестве 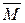: (см. рис).

Задача 2 общая, поэтому она конкретизируется:

2а) Найти минимум линейной функции (или формы) при линейных ограничениях:

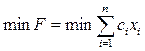при , где j=1–m,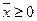

или в матричной форме:

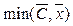при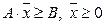

Примером задачи линейного программирования (ЛП) может служить задача о распределении мощности оборудования.

Пусть задано время Т. Требуется выпустить N₁ продукции вида П₁ и N₂ продукции вида П₂ с наименьшими затратами. Пусть имеются две машины А и В, которые могут выпускать как П₁ так и П₂.

Машина	Производительность (продукт/ед. времени)	Время работы машины	Затраты на производство одного изделия в ед. времени
П1	П2	П1	П2	П1	П2
А	a1	a2	x1	x2	a1	a2
В	b1	b2	x3	x4	b1	b2

Математическая постановка задачи:

Требуется минимизировать функцию, учитывающую общие затраты на производство: 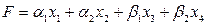при выполнении ограничений:

По времени: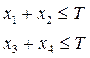
По выпуску: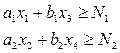

Задача может быть поставлена и по другому, например, это может быть задача о минимизации времени, либо максимизации выпуска продукции и т.д. Однако, нельзя требовать выполнения сразу нескольких условий, т.к. такая задача будет некорректной с математической точки зрения.

2б) Найти минимум ФМП при ограничениях-равенствах.

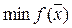при ограничениях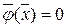

Эта задача получила название классической задачи Лагранжа на условный экстремум.

2в) Найти минимум ФМП при ограничениях-неравенствах.

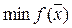при ограничениях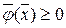

Эта задача называется неклассической задачей. Она конкретизируется следующим образом:

2в-1) Функция 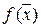– квадратичная, ограничение 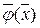– линейная или наоборот. Данная задача называется задачей квадратичного программирования.

Например, имеется два насоса для перекачки жидкости, включенных параллельно. Общий расход воды Q. Мощность, потребляемая машинами, зависит от квадрата объема перекаченной жидкости: 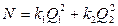, где k₁, k₂ – коэффициенты, характеризующие состояние насосов. 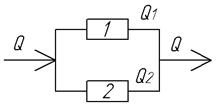Общий объем перекачанной жидкости:

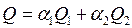
Постановка задачи может быть следующей: либо найти минимум мощности при заданном Q, либо при заданном N найти максимум Q.

2в-2) Функция цели 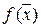является выпуклой и ограничения являются выпуклым множеством. Задача решается методами выпуклого программирования.

2в-3) Функция 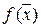и ограничения могут быть любыми. Это задача нелинейного программирования.

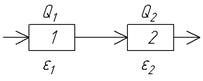Например, пусть при последовательном соединении компрессоров требуется получить максимальную степень сжатия при заданном потреблении мощности. Мощность, потребляемая каждым компрессором, прямо пропорциональная степени сжатия: 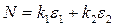, где k₁, k₂ – коэффициенты, характеризующие состояние компрессоров. Общая степень сжатия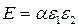

Все рассмотренные задачи объединяются общим термином – задачи математического программирования.

Экстремум функции многих переменных без ограничений

Для функции 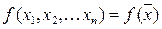справедливо, что если в открытом пространстве функция 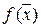имеет в точке х^* минимум (максимум), то эту точку можно окружить такой окрестностью 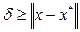, что для всех точек х из d выполняется неравенство 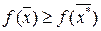(для максимума знак £).

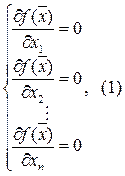Для функции 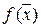справедливо и обобщение теоремы Ферма о необходимом условии существования экстремума в точке х^*, которое говорит о том, что необходимым условием существования экстремума ФМП 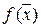в точке х^* является равенство в ней нулю частных производных первого порядка, т.е. в точке х^* справедлива система уравнений (1). Решение этой системы уравнений зависит от вида функции 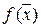. Реальные, снятые экспериментально или полученные аналитически, характеристики объекта управления в инженерной практике, как правило, аппроксимируются так, чтобы порядок функции 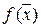был не выше 2-го. При этом возможна аппроксимация:

1. Сепарабельными функциями.

2. Квадратичными (несепарабельными) функциями.

Сепарабельные функции являются частным случаем квадратичных. Они представляются в виде:

,

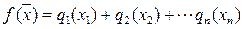т.е. координаты в этой функции развязаны. Примером сепарабельной функции может быть эллиптический параболоид, имеющий уравнение

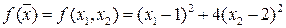, (2)

Квадратичные несепарабельные функции представляются в виде уравнения поверхности второго порядка, которое записывается в матричной форме следующим образом:

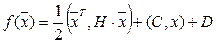
Частным случаем квадратичной функции является квадратичная форма:

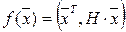
Примером квадратичной функции является следующее уравнение:

, (3)

В матричной форме: 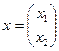, С=(1,1),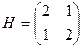

Сделаем проверку:

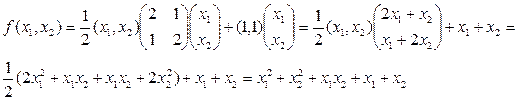
Определение экстремума квадратичных функций

Определить экстремальные точки квадратичных функций можно из условия существования экстремума (1). Для сепарабельных функций экстремальные точки определяются элементарно из уравнений 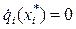. Возьмем для примера функцию (2). Запишем для нее уравнения по правилу (1), из которых получаем точки минимума функции (2).

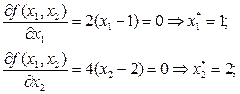
Для несепарабельных квадратичных функций экстремальные точки определяются из решения системы линейных уравнений вида 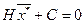, откуда 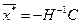. Возьмем для примера функцию (3). Запишем для нее по (1):

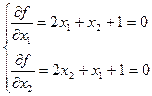
Получили систему линейных уравнений, в которой матрицы Н и С равны:

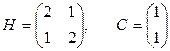
Найдем обратную матрицу ,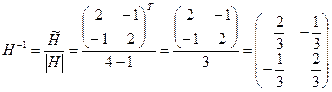

Вычислим 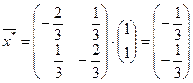– координаты экстремальной точки (минимума).

Вообще говоря, решение системы линейных уравнений не вызывает проблем при хорошо обусловленной матрице Н, когда ее определитель не мал и не велик, как и ее элементы. Но хорошо обусловленные матрицы получаются не всегда при реальных аппроксимациях. Кроме того, операция обращения матрицы довольно громоздкая. Поэтому для поиска экстремума ФМП широкое распространение получили приближенные (численные) методы поиска экстремума. Вторая причина – возможность использования численных методов в автоматических устройствах.

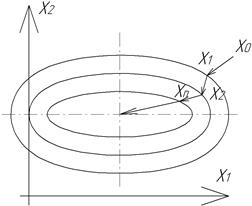
Для ознакомления с этими методами рассмотрим понятия линий уровня. Линии уровня функции 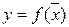получаются из уравнения 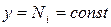. Геометрически для 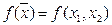это означает, что поверхность рассекается плоскостями, параллельными плоскости (х₁, х₂). В этих плоскостях образуются линии 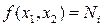, которые проектируются на плоскость (х₁, 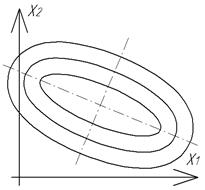х₂). Проекции этих линий называются линиями уровня. 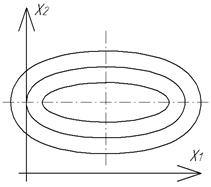Для сепарабельной функции оси линий уровня получаются параллельными осям х₁ и х₂ (т.к. при постоянной одной из координат функция зависит только от другой), а для квадратичной функции оси линий уровня повернуты относительно осей.

Качественное исследование ФМП перед применением численных методов

Прежде чем приступать к численному поиску экстремума функции, необходимо провести качественное исследование функции, т.к. без предварительного анализа свойств функции численные методы поиска экстремума могут не дать желаемых результатов.

На первом этапе определяется сепарабельность или несепарабельность функции по ее виду и локализуется открытое множество М, чтобы в нем был экстремум. При локализации экстремума математика не дает четких правил. Однако инженер, зная характеристики объекта, всегда может провести локализацию необходимого экстремума.

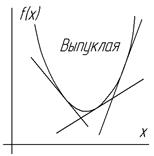
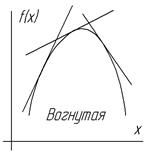Далее нужно знать, единственен ли экстремум и каков его характер, т.е. минимум или максимум. Установление указанных свойств выполняется на основе понятий о выпуклости и вогнутости функций. Четких определений давать не будем, укажем лишь, что для вогнутой функции одной переменной касательная в любой точке этой функции лежит выше этой функции, а для выпуклой функции – касательная в любой точке лежит ниже функции. Математически это записывается следующим образом: 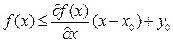(для вогнутой). Для функций многих переменных все аналогично, но только здесь вместо касательных прямых – плоскости (для функции 2-х переменных).

Свойством выпуклых и вогнутых функций является то, что на открытом интервале они имеют единственный экстремум, т.е. каждый локальный экстремум выпуклой функции является ее глобальным минимумом, а каждый локальный экстремум вогнутой функции – максимумом. Это свойство и используется для предварительной локализации экстремальных точек и определения их характера.

Рассмотрим вопрос определения характера экстремума – минимум или максимум. Как известно для функции одной переменной это можно определить по знаку второй производной, если в точке экстремума вторая производная положительная, то это минимум, иначе – максимум. Аналогичным образом решается вопрос о минимуме/максимуме для ФМП. Однако перед этим следует ввести понятия градиента функции и матрицы Гессе.

Если ФМП 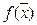дифференцируема, то частные производные первого порядка показывают направление наибольшего возрастания функции 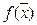в точке 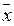. Этот вектор называется градиентом 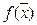в точке 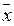и представляет собой вектор-столбец, составленный из частных производных:

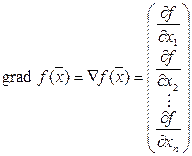
Каждая частная производная определяет проекцию градиента на соответствующую ось. Если взять значение градиента с обратным знаком, то он покажет направление наибольшего убывания функции.

Сейчас возьмем вторые производные от функции 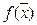. По правилу дифференцирования функциональных матриц получим матрицу:

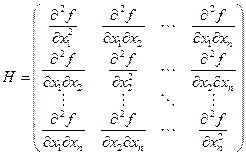
Данная матрица получила название матрицы Гессе, которая является аналогом второй производной для функций одной переменной. Поэтому по знаку матрицы Гессе можно судить о минимуме или максимуме функции, что значительно проще, чем определять это из определения выпуклости или вогнутости функции.

Существует теорема, которая говорит о том, что для выпуклости функции 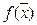необходимо и достаточно, чтобы Н была положительно полуопределена (т.е. равна 0 не только в точке 0, но еще и в других точках). Если Н положительно определена для любог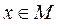о , то 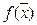– строго выпуклая функция. Для строго вогнутой функции матрица Н должна быть отрицательно определенной для всех .

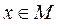Таким образом, если будет показана выпуклость или вогнутость функции 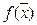, то это будет означать, что на множестве М она будет иметь единственный минимум или максимум. Конструктивная работа с матрицей Гессе зависит от конкретного вида функции 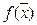. Ранее говорилось о том, что на практике реальные характеристики объектов аппроксимируются сепарабельными или квадратичными функциями, которые в матричной форме можно записать:

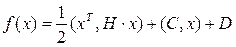
Н в предыдущем уравнении является матрицей Гессе. Для квадратичной формы выпуклость или вогнутость проверяется по матрице Гессе просто, т.к. она состоит только из постоянных коэффициентов. Положительную или отрицательную определенность гессиана можно установить двумя способами.

Первый способ использует критерий Сильвестра, который исследует знаки всех главных миноров Н. Если все главные миноры Н положительны, то матрица Н положительно определена и имеет место выпуклая функция с единственным минимумом. Если же главные миноры отрицательны, то Н отрицательно определена и имеем вогнутую функцию с единственным максимумом.

Пример: Рассмотрим матрицу Н для уравнения (3):

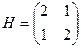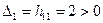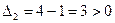, , , следовательно, функция (3) выпуклая и имеет единственный минимум.

Второй способ устанавливает выпуклость или вогнутость функции на базе собственных чисел матрицы Н. Если все собственные числа больше 0, то функция выпуклая, если меньше нуля, то вогнутая.

Покажем это на примере функции (2):

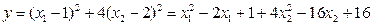, для которой матрица Н:

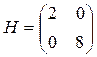
Собственные числа Н:

,

,

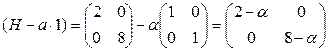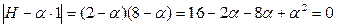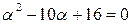
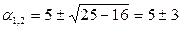, a₁=8>0, a₂=2>0, т.е. (2) – выпуклая функция имеет единственный минимум.

Исследуем выпуклость функции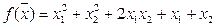

Для нее гессиан: , D₁=2, D₂=0, a₁=4, a₂=0.

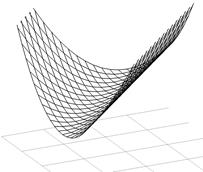Условие строгой выпуклости не выполнено, т.е. Н – положительно полуопределена. Данная поверхность представляет собой бесконечный желоб, и ее минимум будет в любой точке гребня. Такие функции называются слабовыпуклые или слабовогнутые.

Приближенные методы поиска экстремума ФМП без ограничений

Все приближенные методы поиска экстремума ФМП базируются на следующем итерационном (пошаговом) алгоритме:

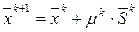, (4)

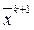по которому переход от точки на к-ом шаге к точке на (к+1)-ом шаге осуществляется в направлении 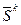с параметром шага в этом направлении m^k. Естественно, что направление 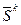следует выбирать таким образом, чтобы приближаться к экстремальной точке. Выбор шага m^k достаточно произволен, но влияет на скорость приближения к экстремуму. Естественно, алгоритм (4) должен быть сходящимся, т.е. гарантировать попадание в экстремум за конечное или бесконечное число итераций. Такая сходимость получила название алгоритмической.

Метод Зейделя-Гаусса (покоординатного спуска)

Сущность метода

Наиболее простым приближенным методом является метод Зейделя-Гаусса. Сущность его заключается в том, что фиксируются все значения координат, кроме одной, по которой и ищется экстремум. Последовательно находя частные экстремумы по координатам за одну или несколько итераций находят приближенное значение координат точки экстремума. В математике доказывается, что метод З-Г сходится для широкого ряда функций, т.е. с его помощью за конечное число итераций можно сколь угодно близко подойти к экстремальной точке. Т.к. метод З-Г использует только необходимые условия, то с его помощью можно найти только локальный экстремум, ближайший к начальной точке. Но т.к. ранее было оговорено, что мы будем рассматривать только выпуклые и вогнутые функции, то экстремум будет глобальным.