Последовательность поиска

1. Прежде всего, отыскивается глобальный экстремум функции 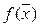, т.е. ведется поиск экстремума без ограничений.

2. В найденной экстремальной точке х^* проверяется выполнение всех ограничений, образующих множество М. Если все ограничения выполняются, то х^* и будет являться решением задачи.

3. Если хотя бы одно из условий нарушается, то условный экстремум находится на границе М. Значит, здесь надо будет уже решать классическую задачу Лагранжа.

Численные методы поиска экстремума ФМП на ограничениях‑неравенствах

Задачи линейного программирования хорошо разработаны и существуют стандартные программы их решения на ЭВМ. Имеется и обширная литература по линейному программированию.

Рассмотрим кратко геометрический способ решения задачи линейного программирования. Специфика задачи ЛП заключается в том, что линейная функция, заданная на замкнутом множестве ограничений, достигает своего наибольшего и наименьшего значений на границах этого множества.

Сформулируем задачу ЛП.

Дана линейная форма F=Cx и система ограничений Ax³B. Среди неотрицательных решений найти такие, которые являются минимумом линейной формы на заданных ограничениях. Задача на максимум приводится к задаче на минимум изменением знака F.

Если система ограничений задана линейными неравенствами, а они определяют выпуклые замкнутые множества, то их пересечение будет выпуклым замкнутым многогранником. На плоскости при n=2 получим выпуклый многоугольник. Следовательно, в ЛП линейная форма задается на замкнутом многограннике. Тогда ее наибольшее и наименьшее значения находятся на границе многогранника: или в вершинах, или на ребрах, или на гранях, причем их число конечно, т.к. конечно число ограничений.

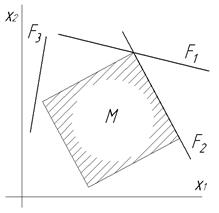Если линейная форма достигает экстремума в вершине (F₁), то решение единственно. Если линейная форма достигает экстремума на ребрах или гранях, то решений будет бесконечное множество (F₂). Возможен случай, когда линейная форма не имеет общих точек с многогранником, тогда решения задачи ЛП не существует (F₃).

Пусть дана функция: 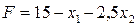и ограничения: 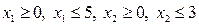. Требования 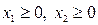вытекают из постановки задачи, т.е. решения должны быть неотрицательными. Требуется найти минимум F.

Построим заданные полупространства ограничений и их пересечение. Полученный четырехугольник является выпуклым, следовательно, решения могут быть только в вершинах или на ребрах многоугольника.

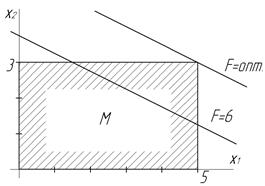Задаемся произвольным значением линейной формы. Пусть F=6. Строится линия 6=15–x₁–2,5x₂, которая не попадает на границу 4‑угольника. Из функции F видно, что для ее уменьшения (а мы ищем минимум) надо увеличивать х₁ и х₂, т.е. следует перемещать прямую F по направлению к правому верхнему углу 4‑угольника на рисунке. Значение F в этой точке F(5,3)=2,5 – минимально. Дальше х₁ и х₂ увеличивать нельзя, т.к. F не будет иметь общих точек с четырехугольником.

Решения 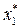и 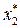называются оптимальным опорным планом, его следует найти. Решение в любой вершине – опорный план. Плоскость F, проходящая через вершину – опорная плоскость.

Поставленную задачу можно решать численно путем перебора всех вершин, при этом используется т.н. симплекс-метод, когда путь к оптимальному опорному плану из некоторого опорного плана осуществляется за минимальное число шагов.

Рассмотрим одну из задач нелинейного программирования – квадратичное программирование – подробнее. Следует отметить, что даже для квадратичного программирования нет эффективных методов. Решение задач проводят только приближенно, при этом использую различные методы поиска, рассмотренные выше.

Задача квадратичного программирования состоит в том, что требуется найти экстремум квадратичной функции 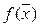при линейных ограничениях-неравенствах 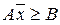. Предполагается, что функция 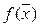выпуклая и задана на выпуклом замкнутом многограннике. В этом случае решение задачи будет единственным.

Рассмотрим одно из направлений численного решения задачи квадратичного программирования, использующее симплексные процедуры (т.е. поиск ведется путем перебора граней, вершин и ребер, если говорить по-русски).

Пусть дана система ограничений вида:

,

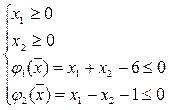и квадратичная целевая функция 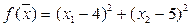, минимум которой нужно найти на данных ограничениях.

На плоскости строится многоугольник, соответствующий заданным ограничениям. Обозначим его ребра через а₁…а₄ и пронумеруем вершины от 1 до 4.

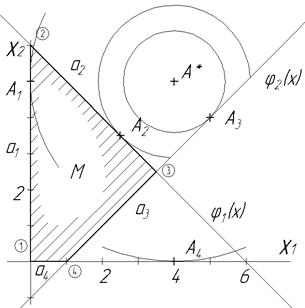Экстремум 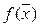может находиться внутри многоугольника или на его границах. Сначала проверяем, находится ли глобальный экстремум внутри многоугольника. Из необходимых условий экстремума находим:

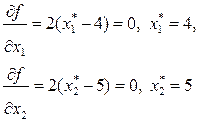
Для точки х^* проверяются ограничения. Условия 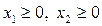выполняются. 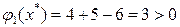– не выполняется, 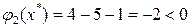– выполняется. Т.к. условие 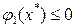не выполнилось, точка абсолютного экстремума не принадлежит многоугольнику. Эта точка на рисунке обозначена А^*.

Теперь следует определить на каких гранях или вершинах 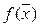достигает минимума. Т.к. число вершин и ребер конечно, то за конечное число итераций будет найдена экстремальная точка.

Будем определять экстремум 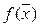на ребрах используя метод Лагранжа.

а₁) Для ребра а₁ (ограничение х₁=0)

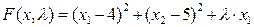
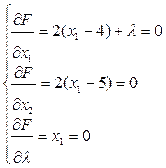
Получим точку А₁=(0, 5), которая принадлежит М, значит является подозрительной на экстремум. f(A₁)= 16.

а₂) Ограничение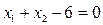

, , .

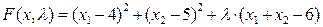
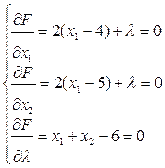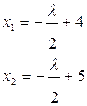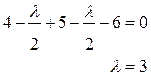Получили точку А₂=(2,5; 3,5), которая принадлежит М. f(A₂)= 4,5.

а₃) Ограничение .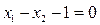

, , .

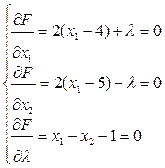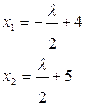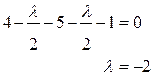Получили экстремальную точку на а₃ – А₃=(5, 4), не принадлежащую многоугольнику, поэтому точку А₃ выбрасываем из дальнейшего расчета.

вершина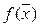
	6,5

а₄) Для ребра а₄ (х₂=0) по аналогии с ребром а₁ можно найти экстремальную точку А₄=(4, 0), не принадлежащую М.

Сравнивая значения функции в точках А₁ и А₂ приходим к выводу, что минимум достигается в точке А₂. Теперь остается проверить значения функции в вершинах многоугольника. Проверка показывает, что значения 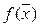в вершинах будут больше, чем значение функции в точке А₂. Следовательно, данная точка и является решением задачи.

Для решения задач нелинейного программирования применяются те же методы поиска экстремума, что были рассмотрены ранее.