Наконец, параметр m можно задавать постоянным на всех итерациях. Однако при больших значениях m процесс поиска может расходиться. Хорошим способом выбора m может быть его определение на первой итерации из условия экстремума по направлению градиента. На последующих итерациях m остается постоянным. Это еще более упрощает вычисления.
Например, для функции 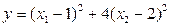 при
при 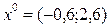 с проекциями градиентов
с проекциями градиентов 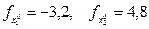 методом наискорейшего спуска определен
методом наискорейшего спуска определен 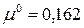 . Примем параметр
. Примем параметр 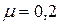 постоянным на всех итерациях.
постоянным на всех итерациях.
Вычисляем координаты х(1):
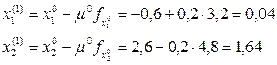
Для вычисления координат точки х(2) находим проекции градиента в точке х(1): 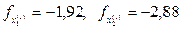 , тогда
, тогда
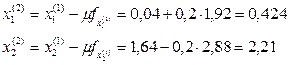 и т.д.
и т.д.
Данная последовательность также сходится.
Шаговый градиентный метод
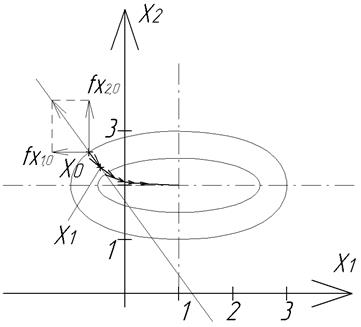 Этот метод разработан инженерами и заключается в том, что шаг по одной из переменных берется постоянным, а для других переменных он выбирается исходя из пропорциональности градиентов точках. Этим как бы масштабируют экстремальную поверхность, т.к. не по всем переменным сходимость одинакова. Поэтому выбором различных шагов для координат пытаются сделать скорость сходимости примерно одинаковой по всем переменным.
Этот метод разработан инженерами и заключается в том, что шаг по одной из переменных берется постоянным, а для других переменных он выбирается исходя из пропорциональности градиентов точках. Этим как бы масштабируют экстремальную поверхность, т.к. не по всем переменным сходимость одинакова. Поэтому выбором различных шагов для координат пытаются сделать скорость сходимости примерно одинаковой по всем переменным.
Пусть дана сепарабельная функция 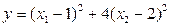 и начальная точка
и начальная точка 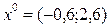 . Зададимся постоянным шагом по координате х1, пусть Dх1=0,2. Шаг по координате х2 находим из соотношения градиентов и шагов:
. Зададимся постоянным шагом по координате х1, пусть Dх1=0,2. Шаг по координате х2 находим из соотношения градиентов и шагов:
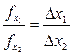 , тогда
, тогда 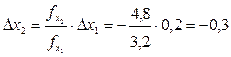
Координаты точки х(1): 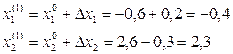
Теперь определяется Dх2 для второй итерации:
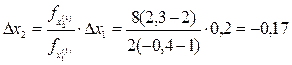
Координаты х(2): 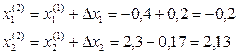
Продолжая вычисления, получим:
| Итерация | ||||||
| х1 | 0,2 | 0,4 | 0,6 | 0,8 | ||
| х2 | 2,044 | 2,008 |
На девятой итерации получили х(8)=(1,2). При попытке вычислить Dх2 получим:
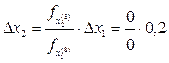 – неопределенность, т.к. проекции градиентов равны 0, т.е. мы попали в экстремальную точку – итерации можно завершить.
– неопределенность, т.к. проекции градиентов равны 0, т.е. мы попали в экстремальную точку – итерации можно завершить.
Шаговый градиентный метод не обладает свойством сходимости, но весьма эффективен.
Метод сопряженных направлений
В заключение изучения приближенных методов поиска экстремума ФМП без ограничений рассмотрим метод сопряженных направлений, который завоевывает на практике все большую популярность.
Сначала дадим понятие сопряженности. Пусть имеем два направления, которые характеризуются векторами 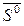 и
и 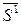 . Направления
. Направления 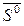 и
и 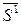 называют сопряженными по отношению к некоторой положительно определенной матрице Н, если выполняется соотношение
называют сопряженными по отношению к некоторой положительно определенной матрице Н, если выполняется соотношение
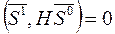 , (7)
, (7)
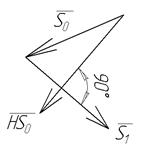 Сопряженность связана с ортогональностью. Если Н – единичная матрица, то при
Сопряженность связана с ортогональностью. Если Н – единичная матрица, то при 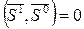 имеем два взаимно перпендикулярных вектора. Соотношение (7) можно трактовать таким образом: матрица Н, примененная к вектору
имеем два взаимно перпендикулярных вектора. Соотношение (7) можно трактовать таким образом: матрица Н, примененная к вектору 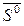 , изменяет его длину и поворачивает на некоторый угол так, что новый вектор
, изменяет его длину и поворачивает на некоторый угол так, что новый вектор 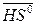 должен быть ортогонален вектору
должен быть ортогонален вектору 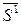 .
.
С помощью метода сопряженных направлений отыщем экстремум сепарабельной функции 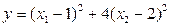 с начальной точкой
с начальной точкой 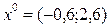 .
.
1) Производится выбор 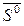 и в этом направлении отыскивается экстремум.
и в этом направлении отыскивается экстремум.
Возьмем вектор 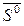 с направлениями
с направлениями 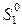 и
и 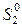 . Вектор
. Вектор 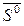 можно выбирать произвольно, поэтому возьмем
можно выбирать произвольно, поэтому возьмем 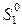 =
= 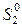 =1. Вектор
=1. Вектор 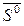 дает направление L1.
дает направление L1.
Проведем через L1 плоскость перпендикулярную плоскости {x1, x2}. Плоскость пересечет экстремальную поверхность у(х1, х2) и выделит на ней экстремальную линию. Определим координаты минимума на этой линии (параболе), для чего вычислим проекции градиента в точке х0:
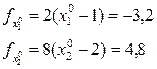 ,
,
и по формуле (6) найдем m:
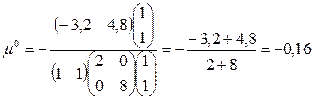
Тогда:
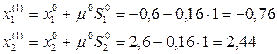
Естественно, линия L1 касается в точке х(1) линии равного уровня функции у.
2) Отыскивается 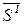 из условия сопряженности
из условия сопряженности 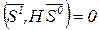 .
.
Получим сопряженный вектор 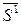 с проекциями
с проекциями 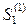 и
и 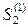 , воспользовавшись формулой (7):
, воспользовавшись формулой (7):
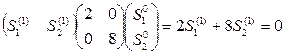
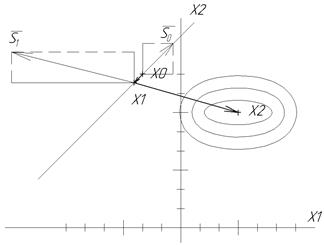 Получили одно уравнение с двумя неизвестными. Т.к. нам требуется только направление вектора
Получили одно уравнение с двумя неизвестными. Т.к. нам требуется только направление вектора 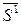 , а не его длина, то одним из неизвестных можно задаться произвольно. Пусть
, а не его длина, то одним из неизвестных можно задаться произвольно. Пусть 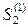 =1, тогда
=1, тогда 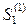 = –4.
= –4.
3) Из точки х(1) в направлении 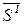 ищется экстремум.
ищется экстремум.
Сопряженный вектор должен проходить через х(1). Сделаем шаг в сопряженном направлении:
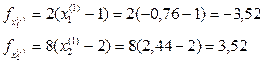
Величина шага m(1) в х(1):
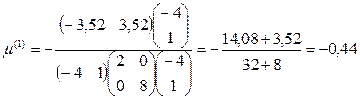 ,
,
тогда
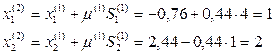
Итак, за две итерации было найдено точное значение экстремума функции у. В качестве первого вектора  можно было выбрать градиент в исходной точке, процедура поиска остается при этом прежней.
можно было выбрать градиент в исходной точке, процедура поиска остается при этом прежней.
В математике доказывается, что метод сопряженных направлений сходится для квадратичных функций не более чем за n итераций, где n – число переменных. Данное обстоятельство особенно ценно для практики, поэтому данный метод находит все большее применение.
Для функций более общего вида метод сопряженных направлений пока еще только разрабатывается. Основное затруднение тут состоит в том, что матрица Гессе получается функциональной, т.е. содержит переменную.
Классическая задача Лагранжа на условный экстремум (ограничения-равенства).
 Пусть задана целевая функция
Пусть задана целевая функция 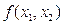 и ограничение-равенство (уравнение связи)
и ограничение-равенство (уравнение связи) 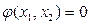 . Требуется найти минимум
. Требуется найти минимум 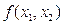 на множестве
на множестве 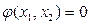 . Считаем, что функции
. Считаем, что функции 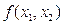 и
и 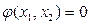 имеют непрерывные первые производные и являются выпуклыми или вогнутыми.
имеют непрерывные первые производные и являются выпуклыми или вогнутыми.
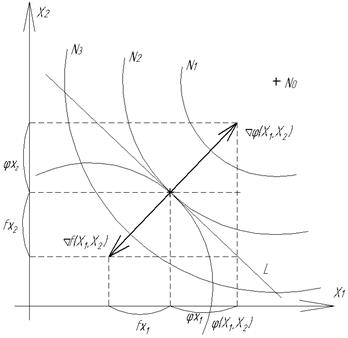
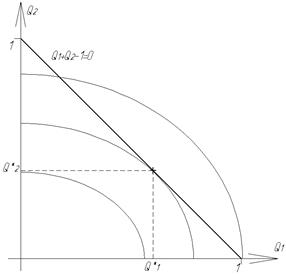
Рассмотрим геометрическую интерпретацию классической задачи. На плоскости {x1, x2} построим функцию 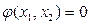 , а также линии равного уровня функции
, а также линии равного уровня функции 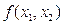 со значениями N1<N2<…Nn. Линия N1 не имеет общих точек с
со значениями N1<N2<…Nn. Линия N1 не имеет общих точек с 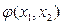 , линия N3 имеет 2 общих точки с
, линия N3 имеет 2 общих точки с 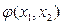 и они не могут быть решением задачи, т.к. N3> N2. Остается линия уровня N2, которая имеет единственную точку касания с
и они не могут быть решением задачи, т.к. N3> N2. Остается линия уровня N2, которая имеет единственную точку касания с 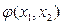 . Абсолютный минимум N0 может не принадлежать ограничению
. Абсолютный минимум N0 может не принадлежать ограничению 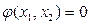 и поэтому не может быть решением задачи. Отсюда ясно и название «условный экстремум», т.е. такой экстремум, который достигается только на заданных ограничениях.
и поэтому не может быть решением задачи. Отсюда ясно и название «условный экстремум», т.е. такой экстремум, который достигается только на заданных ограничениях.
В точке касания 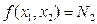 с функцией
с функцией 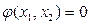 проведем касательную линию L. Поострим градиенты функций
проведем касательную линию L. Поострим градиенты функций 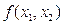 и
и 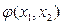 в точке касания, они будут лежать на одной линии, т.к. оба перпендикулярны L и направлены в разные стороны. Определим проекции градиентов на оси х1 и х2 в точке касания:
в точке касания, они будут лежать на одной линии, т.к. оба перпендикулярны L и направлены в разные стороны. Определим проекции градиентов на оси х1 и х2 в точке касания:
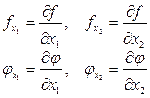
Из подобия треугольников можно записать:
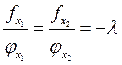 – множитель Лагранжа.
– множитель Лагранжа.
или 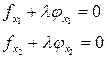
Составим теперь функцию 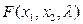 следующим образом:
следующим образом:
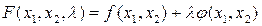 – функция Лагранжа.
– функция Лагранжа.
Запишем соотношения для нахождения экстремума функции F.
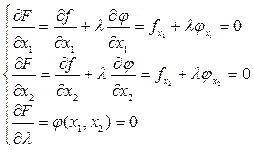
Как видно, получили те же соотношения, что были получены исходя из геометрической интерпретации задачи. Постоянная l называется множителем Лагранжа. С помощью этого множителя задача на условный экстремум сводится к задаче на безусловный экстремум.
В общем случае, число переменных примем за n, а число ограничений за m. Тогда функция Лагранжа запишется в виде:
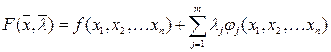
или в векторной форме
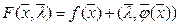
Для решения задачи записывается система уравнений:
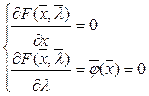 , (8)
, (8)
т.е. для n+m переменных будем иметь n+m уравнений. Если система совместна, то задача Лагранжа имеет единственное решение.
Т.к. для определения экстремума использовались только первые производные, то полученные условия будут являться только необходимыми. Если функции 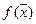 и
и 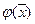 выпуклые или вогнутые, то условный экстремум единственный. Если одна из функций невыпуклая, то экстремум может быть и не единственным. Кроме того, открыт вопрос о том, что найдено – минимум или максимум, хотя в инженерной практике обычно из физических соображений это бывает ясно.
выпуклые или вогнутые, то условный экстремум единственный. Если одна из функций невыпуклая, то экстремум может быть и не единственным. Кроме того, открыт вопрос о том, что найдено – минимум или максимум, хотя в инженерной практике обычно из физических соображений это бывает ясно.
Пример: Покажем технику решения задачи методом Лагранжа.
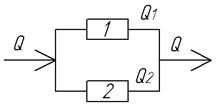 Для рассмотренного выше примера с двумя насосами, задан объем перекачиваемой жидкости:
Для рассмотренного выше примера с двумя насосами, задан объем перекачиваемой жидкости:
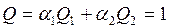
При этом ограничении требуется найти потребляемую мощность насосов 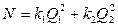 . Пусть коэффициенты равны a1=a2=1, К1=1, К2=1,5. Тогда целевая функция
. Пусть коэффициенты равны a1=a2=1, К1=1, К2=1,5. Тогда целевая функция 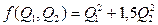 , найти минимум при ограничении:
, найти минимум при ограничении: 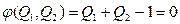 .
.
Процедура решения:
1. Составляем функцию Лагранжа
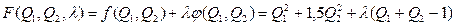
2. Составляется система уравнений (8):
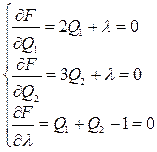
3. Записываются Qi через l и подставляются в третье выражение:
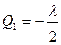 ,
, 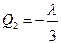 ,
, 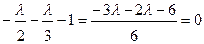 ,
, 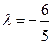
Тогда координаты экстремума:
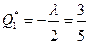 ,
, 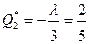
Пример 2:
Пусть дано последовательное соединение компрессоров.  Задана требуемая степень сжатия:
Задана требуемая степень сжатия: 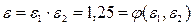 , которую требуется обеспечить при минимуме расхода мощности:
, которую требуется обеспечить при минимуме расхода мощности:
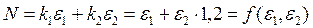
Решение:
1. 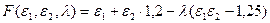
2. 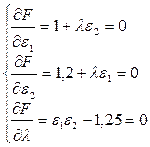
3. 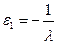 ,
, 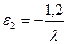 , подставляем в выражение для
, подставляем в выражение для 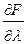 :
:
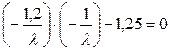 ,
, 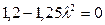 ,
, 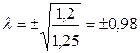 . Из физических соображений положительный корень отбрасываем, поэтому l= –0,98.
. Из физических соображений положительный корень отбрасываем, поэтому l= –0,98.
Тогда координаты экстремума:
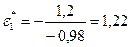 ,
, 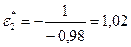
Как видно из приведенных примеров при решении задачи Лагранжа получаем в общем случае систему нелинейных уравнений, которую подчас трудно решить аналитически. Поэтому целесообразно применять приближенные методы решения задачи Лагранжа.
Приближенные методы решения классической задачи Лагранжа на условный экстремум
Первый метод численного решения задачи Лагранжа основан на соотношении Лагранжа:
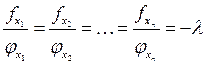
т.е. только в экстремальной точке все соотношения градиентов функций равны. Это соотношение и используется при поиске экстремума.
Пример:
По первому методу решим задачу поиска экстремума функции 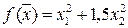 при ограничении
при ограничении 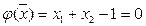 .
.
Отношение проекций градиентов функции 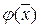 равно
равно 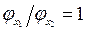 , следовательно, отношение проекций градиентов функции
, следовательно, отношение проекций градиентов функции 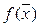 в экстремальной точке х* должно быть равно
в экстремальной точке х* должно быть равно
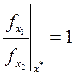
Проекции градиентов функции 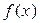 в произвольной точке равны:
в произвольной точке равны: 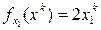 ,
, 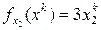 . В качестве начальной точки примем х0=(0,2; 0,8), в которой
. В качестве начальной точки примем х0=(0,2; 0,8), в которой 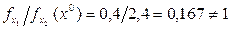 . Возьмем шаг по координате х1 Dх1=0,2.
. Возьмем шаг по координате х1 Dх1=0,2.
Если в качестве первого приближения взять точку (0, 1), то в ней соотношение 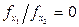 , т.е. шаг был сделан не в ту сторону (т.к. требуется двигаться в сторону равенства
, т.е. шаг был сделан не в ту сторону (т.к. требуется двигаться в сторону равенства 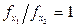 ). Следовательно нужно идти в сторону увеличения х1.
). Следовательно нужно идти в сторону увеличения х1.
Результаты вычислений запишем в таблицу:
| хк | 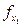 | 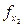 | Соотношение 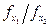 |
| (0,2; 0,8) | 0,4 | 2,4 | 0,167 |
| (0,4; 0,6) | 0,8 | 1,8 | 0,444 |
| (0,6; 0,4) | 1,2 | 1,2 |
Таким образом, на третьей итерации получили экстремальную точку.
 2015-06-26
2015-06-26 1885
1885
