Применение метода З-Г к сепарабельным функциям

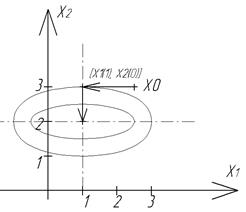
Пусть задана функция 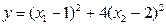. Ранее было показано, что это строго выпуклая функция с минимумом в точке х^*=(1, 2). Однако при использовании приближенных методов значения координат экстремума не известны (иначе задача теряет смысл). Проиллюстрируем метод З-Г на плоскости. На рисунке изображены линии уровня функции (2).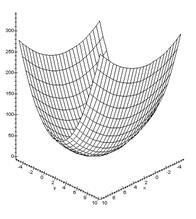

Пусть задана точка х⁰=(2,5; 3), начальная точка может быть любой, т.к на функцию не наложено ограничений. Зафиксируем координату 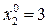. Это равноценно проведению в пространстве {y, x₁, x₂} плоскости П₀, параллельной плоскости {y, x₁}. Запишем уравнения функции в этой плоскости:

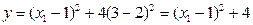
Следовательно, в плоскости П₀ функция является параболой. Найдем координаты экстремума в плоскости П₀, 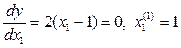. Определим значение функции при 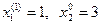: y=4.

Теперь зафиксируем точку x₁ на ее экстремальном значении, полученном на предыдущем шаге 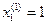. Это равносильно проведению плоскости П₁ параллельно плоскости {y, x₂}. В данной плоскости функция является параболой с уравнением: 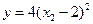. Найдем координаты экстремума в плоскости П₁: .

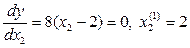Таким образом, за одну итерацию, содержащую два шага, найдено точное значение экстремума сепарабельной функции. Это объясняется тем, что главные оси эллипсов, являющихся линиями уровня, были параллельны осям x₁ и x₂. Данное правило распространяется и на функции n переменных. Если уравнение сепарабельной функции содержит n переменных, то для нахождения ее экстремума требуется не более n шагов. В этом огромное преимущество метода З-Г для сепарабельных функций.