Доказательство. Пусть f(x1,,xn) 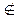M. Тогда найдутся такие два набора 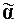и

Пусть f (x ₁,...,x _n) M. Тогда найдутся такие два набора и 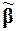значений переменных x ₁,..., x_n, что 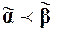и 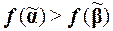. Возьмем эти наборы. Предположим, что они различаются в k компонентах.

Построим цепочку двоичных наборов, последовательно заменяя значения 0, 1,..., k разрядов, в которых набор 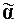отличается от набора :

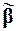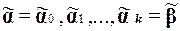. (1)

Очевидно, что всякие два соседних набора этой последовательности различаются ровно в одной компоненте.

Рассмотрим значения f на наборах цепочки (1).

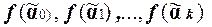. (2)

Поскольку 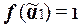и 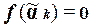, то в (2) найдутся последовательно идущие значения 1 и 0.

Рассмотрим наборы 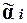= 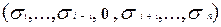и 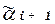= = 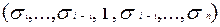, на которых функция f принимает значения 1 и 0.

Тогда .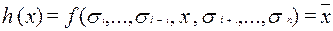

Действительно,

h (0) = h 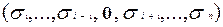= 1 и

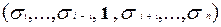h (1) = h )= 0.

Доказательство окончено.

Замечание. Двоичные наборы, различающиеся лишь в одной компоненте, называются соседними. Доказательство последней леммы позволяет утверждать, что для всякой немонотонной функции найдутся таких два соседних набора, на которых нарушается монотонность.

Рассмотрим пример использования леммы о немонотонной функции. Пусть задана функция f = x ₁ ® (x ₂® x ₃). Тогда наборы
(0, 1, 0) и (1, 1, 0) являются соседними и на этих наборах нарушается монотонность f:

f (0, 1, 0) = 1 и f (1, 1, 0) = 0.

Поэтому f (x, 1, 0) = .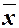

Упражнение.

1. Докажите утверждение, обратное утверждению, сформулированному в лемме о немонотонной функции.

2. Проверьте справедливость следующего утверждения: Если ф.а.л. f (x ₁,...,x _n) отличнаот тождественной единицы, то всякая минимальная ДНФ для f не содержит элементарных конъюнкций, содержащих отрицания переменных.