Пусть f 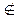 S. Тогда найдётся таких два противоположных набора
S. Тогда найдётся таких два противоположных набора 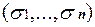 и
и 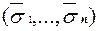 , что f
, что f 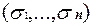 = f
= f 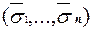 . Определим вспомогательные функции:
. Определим вспомогательные функции:
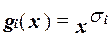 , где i = 1,..., n.
, где i = 1,..., n.
Тогда функция h (x) = f (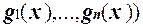 совпадает с одной из функций констант.
совпадает с одной из функций констант.
Определим значения h (0) и h (1):
h (0) = f (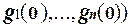 = f
= f 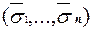 .
.
h (1) = f (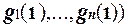 = f
= f 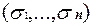 .
.
Следовательно, h (0) = h (1).
Доказательство окончено.
Замечание. Поскольку функции-константы не являются самодвойственными, то доказанная лемма утверждает, что из любой несамодвойственной функции можно получить простейшую несамодвойственную функцию.
Упражнение. Доказать утверждение, обратное утверждению, сформулированному в лемме о несамодвойственной функции.
 2015-06-26
2015-06-26 322
322








