Рассмотрим функцию f 0. По определению f 0(0,..., 0) = 1.
Если f 0(1,..., 1) = 1, то h (x) = f 0(x,..., x) = 1, т.е. это функция, получаемая из f 0 отождествлением всех переменных, является константой 1. В противном случае f 0(1,..., 1) = 0. Поэтому f 0(x,..., x) = 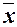 . Тогда по лемме о несамодвойственной функции из f 0 с помощью функции отрицания и тождественной функции можно получить одну из констант.
. Тогда по лемме о несамодвойственной функции из f 0 с помощью функции отрицания и тождественной функции можно получить одну из констант.
Вторая константа получается из первой константы с помощью отрицания (т.е. является отрицанием первой константы).
Значит, из f 0 можно получить либо одну из констант, либо обе константы и отрицание.
Рассмотрим функцию f 1. По определению этой функции f 1(1,..., 1) = 0. Если f 1(0,..., 0) = 0, то f 1(x,..., x) = 0, т.е. это функция-константа 0.
В противном случае f 1(0,..., 0) = 1 и f 1(x,..., x) = 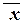 . Тогда из леммы о несамодвойственной функции следует, что из f 1 можно получить одну из констант. Вторая константа получается из первой константы с помощью функции
. Тогда из леммы о несамодвойственной функции следует, что из f 1 можно получить одну из констант. Вторая константа получается из первой константы с помощью функции 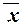 .
.
Поэтому из f 0 и f 1 с помощью отождествления переменных всегда можно выразить обе функции-константы, а в некоторых случаях еще и функцию отрицания.
4.14.2. Построение отрицания
Рассмотрим функцию fM. По лемме о немонотонной функции через fM с помощью функций-констант и тождественной функции x можно выразить отрицание 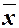 .
.
4.14.3.Построениеконъюнкции
Рассмотрим функцию fL. По лемме о нелинейной функции из fL с помощью уже полученных функций 0, 1, 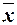 и обозначений переменных можно выразить конъюнкцию x 1& x 2.
и обозначений переменных можно выразить конъюнкцию x 1& x 2.
Следовательно, через функции системы B можно выразить функции полной системы 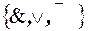 . Тогда на основании теоремы редукции можно утверждать, что B - это полная система.
. Тогда на основании теоремы редукции можно утверждать, что B - это полная система.
Доказательство окончено.
Упражнение.
Используя доказательство критерия полноты, выразить функции x 1& x 2 и 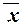 через функции полной системы
через функции полной системы 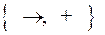 .
.
Достоинство доказанной теоремы по сравнению с теоремой редукции состоит в том, что теперь полнота произвольной системы, булевских функций может быть установлена на основании проверки простых свойств у функции системы.
При этом если система B является конечной, то такая проверка может быть проведена за конечное время.
Для проверки полноты произвольной конечной системы B можно построить таблицу со строками, соответствующими функциям системы B, и пятью столбцами, соответствующими пяти классам: Т 0, Т 1, S, L и M.
Таблица заполняется символами " + " и " - ". Некоторый элемент таблицы это " + ", если функция, соответствующая строке, содержится в классе функций, соответствующем столбцу. В противном случае элемент таблицы равен "-".
Если в каждом столбце полученной таблицы имеется хотя бы один минус, то B - это полная система.
Если в таблице имеется столбец, содержащий только символы " + ", то B - это неполная система.
Например. Для системы B = { x 1 ® x 2, x 1 + x 2} таблица имеет вид:
| Т0 | Т1 | S | L | M | |
| x 1 ® x 2 | - | + | - | - | - |
| x 1 + x 2 | + | - | - | + | - |
Следовательно, множество функций { x 1 ® x 2, x 1 + x 2} - это полная система.
Классы Т 0, Т 1, S, L и M объединяет одно общее свойство, которое состоит в том, что всякий из них является "почти" полным.
 2015-06-26
2015-06-26 2608
2608








