2015-06-26
341
ИЗУЧЕНИЕ РЕЗОНАНСА НАПРЯЖЕНИЙ
Цель работы: 1. Усвоение и получение навыка применения закона Ома для цепей переменного тока.
2. Изучение установившихся вынужденных колебаний в цепях переменного тока.
3. Изучение явления резонанса.
Приборы и принадлежности: генератор, цифровой вольтметр, амперметр, плата с набором различных емкостей (конденсаторов) и катушки индуктивности.
Теоретическая часть
Пусть цепь (рис. 1), содержащая последовательно соединенные активное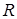 
, индуктивное 
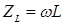и емкостное 
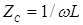сопротивления, питается от источника переменного тока
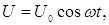(1)
где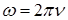 
- круговая частота тока (
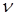- частота тока), 
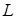- индуктивность цепи, 
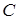- электроемкость цепи.
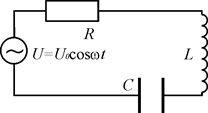
Р и с. 1
В цепи возникает переменный ток, который вызовет на всех элементах цепи соответствующие падения напряжения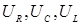 
. Причем,
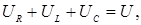(2)
где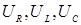 
- мгновенные значения напряжения на активном сопротивлении, индуктивности и емкости нашей цепи, 
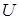- мгновенное значение напряжения, подведенного к цепи.
Для решения уравнения (2) воспользуемся так называемым методом векторных диаграмм.
Метод векторных диаграмм основан на том, что косинусоидально изменяющуюся со временем величину можно представить в виде проекции на горизонтальную ось вращающегося вектора, длина которого равна максимальному значению косинусоидально изменяющейся величины, угловая скорость вращения вектора равна круговой частоте колебаний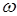 
, а угол, образованный вектором с горизонтальной осью в начальный момент времени равен начальной фазе 
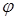нашей косинусоидальной величины.
За основу построения векторной диаграммы примем направление вектора тока. Учтем, что напряжение на сопротивлении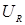 
совпадает по фазе с силой тока и равно:
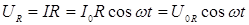. (3)
Напряжение на индуктивности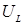 
опережает силу тока на 
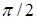и равно:
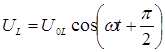, (4)
где 
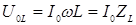, а 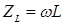- индуктивное сопротивление.
Напряжение на конденсаторе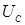 
отстает от силы тока на 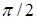и равно:
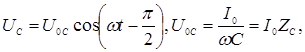(5)
где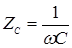 
- емкостное сопротивление.
Подставим выражения (3), (4) и (5) в левую часть уравнения (2) и при этом, учтем, что сумма косинусоидальных колебаний одинаковой частоты с разными начальными фазами даст косинусоидальное колебание той же частоты, максимальное значение и начальная фаза которого зависит от максимальных значений и начальных фаз слагаемых колебаний.
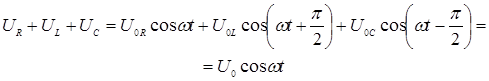(6)
Для сложения этих трех гармонических колебаний воспользуемся векторной диаграммой напряжений (рис.2). Колебания напряжения на сопротивлении изображаются на ней вектором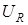 
, направленном вдоль оси токов, колебания же напряжения на индуктивности и емкости - векторами, перпендикулярными к оси токов, с длинам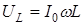и 
и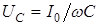 
. Складывая два последних колебания, получим одно, изображаемое вектором 
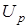, перпендикулярном к оси токов и имеющим длину: 
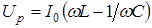. Полное напряжение можно рассматривать как сумму двух гармонических колебаний: напряжения 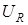, совпадающего по фазе с током, и напряжения 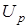, отличающегося по фазе на 
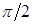. Первое получило название активной составляющей, а второе 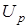- реактивной составляющей. Оба эти колебания, складываясь, дают гармоническое колебание: 
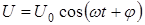. Оно изображается суммой вектором 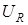и 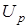, причем длина результирующего вектора равна амплитуде напряжений 
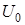, а угол, образованный результирующим вектором с осью токов - сдвигу фазы между током и напряжением .
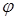На рис. 2. представлена векторная диаграмма амплитуд падения напряжения на сопротивлении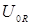 
, катушке индуктивности 
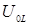и конденсаторе 
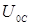. Амплитуда приложенного напряжения 
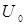должна быть равна векторной сумме амплитуд этих падений напряжений.
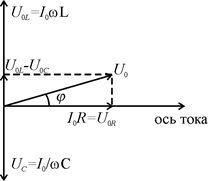
Р и с. 2.
Тогда максимальное значение подведенного к цепи напряжения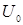 
и сдвиг фаз 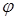между напряжением и током получается из векторной диаграммы равными:
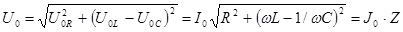, (6)
а 
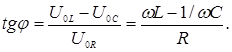(7)
Следует учесть, что электроизмерительные приборы в цепях переменного тока измеряют не амплитуду значения тока и напряжения, а их эффективные значения:
, 
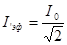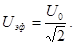
Выражение (6) представляет собой закон Ома цепи переменного тока с последовательным соединением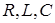 
, где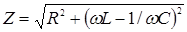 
- полное сопротивление цепи переменному току. Из анализа уравнения (6) следует:
1. Сопротивление цепи зависит не только от параметров 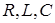, но и от круговой частоты 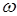переменного тока.
2. Для данных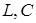 
можно подобрать 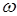таким образом, чтобы 
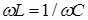. При этом разность 
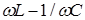обращается в ноль и значение тока в цепи достигает своей максимальной величины 
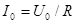, а сдвиг фаз между током и напряжением цепи обращается в ноль. Это явление называют резонансом напряжений (на индуктивности и емкости), а частота 
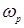, при которой достигается резонанс - резонансной частотой.
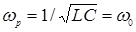(8)
Таким образом, резонанс напряжений возникает при равенстве индуктивного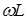 
и емкостного 
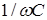сопротивлений в цепи переменного тока при их последовательном соединении.
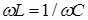- условие резонанса. (9)
Отсюда видно, что явление резонанса может быть достигнуто тремя способами:
1. Изменением частоты 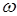при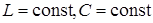 
.
2. Изменением индуктивности цеп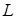и при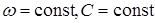 
3. Изменением емкости цеп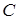и при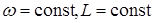 
.
Следует учитывать, что при резонансе напряжений возможно возникновение высоких напряжений на индуктивности и емкости (больших напряжения, подведенного ко всей цепи).
Действительно, при резонансе
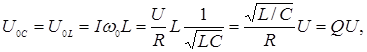
где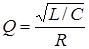 
- добротность контура, т. е. при резонансе амплитуда напряжения на реактивных элементах 
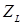и 
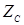в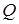 
раз больше приложенного напряжения 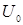. Как правило 
.
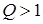Если при заданных 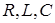изменить 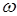, то, учитывая формулу (9) получим ряд значений тока, которые будучи отложены на графике 
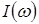дадут кривую зависимости тока от частоты (рис. 3).
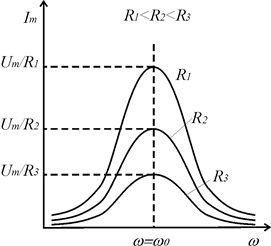
Р и с. 3
Эта кривая называется резонансной кривой. Она имеет максимум при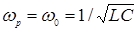 
. Характер резонансной кривой при данном 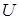будет зависеть от величины активного сопротивления 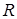. Чем меньше 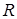, тем кривая более крутая и острая (острый резонанс) и чем больше 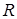, тем положе кривая (тупой резонанс).
