Изучение резонанса напряжений в цепях переменного тока

ЛАБОРАТОРНАЯ РАБОТА

№ 2.5a

ИЗУЧЕНИЕ РЕЗОНАНСА

НАПРЯЖЕНИЙ

МЕТОДИЧЕСКОЕ ПОСОБИЕ

Минск 2011

ИЗУЧЕНИЕ РЕЗОНАНСА НАПРЯЖЕНИЙ

Цель работы. Изучить явление резонанса в цепях переменного тока. Определить резонансные частоты и параметры цепей для различных типов соединений.

Изучение резонанса напряжений в цепях переменного тока

Резонанс напряжений возникает при определенных условиях в цепи переменного тока с последовательно соединенным активным сопротивлением R, соленоидом индуктивностью L и конденсатором емкостью C (рис. 1).

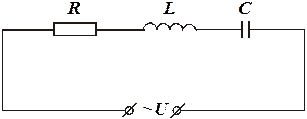
Рис. 1

Пусть цепь подключена к источнику синусоидального напряжения U, которое изменяется с циклической частотой w = 2pf. По закону Кирхгофа для данной цепи

u_R + u_C = u + e_L (1)

или

iR + q/C + Ldi/dt = u (2)

Дифференциальное уравнение (2) можно решить различными методами. используем для его решения метод векторных диаграмм.

Эту же задачу можно решить методом векторных диаграмм. Этот метод основан на том, что синусоидально изменяющуюся со временем величину (например, a = A₀ sin(wt + j) графически можно предоставить в виде проекции на вертикальную ось вращающегося вектора, длина которого равна максимальному (амплитудному) значению А₀. Угловая скорость вращения вектора равна циклической частоте w, а угол, образованный вектором с горизонтальной осью в начальный момент времени, равен начальной фазе j синусоидальной величины (рис. 2).

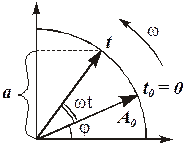
Рис. 2

Пользуясь методом векторных диаграмм, можно алгебраическое сложение мгновенных значений синусоидально изменяющихся со временем величин одинаковой частоты заменить геометрическим сложением векторов их представляющих. Тогда длина результирующего вектора даст амплитуду результирующей синусоиды, а угол, образованный им с горизонтальной осью - ее начальную фазу.

Построим векторную диаграмму напряжений нашей цепи. Для этого заметим, что если источник в цепи создает синусоидальное напряжение u, изменяющееся с частотой w, то ток в цепи будет также синусоидальным с той же частотой. Поскольку ток в последовательной цепи на всех участках одинаков, то удобнее принять начальную фазу тока равной нулю, а напряжения на участках цепи рассчитать при этом условии.

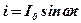, (3)

где I₀ - амплитуда тока. Тогда мгновенное значение напряжения на активном сопротивлении

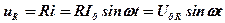, (4)

т.е. совпадает по фазе с силой тока, где U_0R = RI₀ - амплитуда напряжения на активном сопротивлении R.

Мгновенное значение напряжения на индуктивности

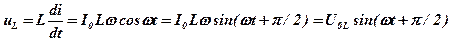, (5)

т.е. опережает по фазе силу тока на p/2, где U_0L = I₀Lw - амплитуда напряжения на катушке индуктивности L.

Мгновенное значение напряжения на емкости

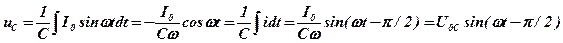, (6)

т.е. отстает по фазе от силы тока на p/2, где U_0С = I₀/Cw - амплитуда напряжения на емкости С.

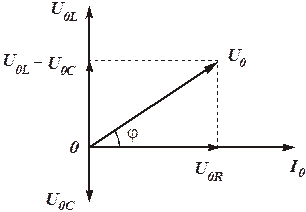
Рис. 3

При построении векторной диаграммы вектор тока откладывается горизонтально, поскольку он одинаков во всех последовательно соединенных элементах цепи R, L и C. Вектора, соответствующие напряжениям, представляются с учетом соответствующего сдвига фаз относительно тока (рис. 3).

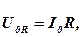
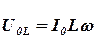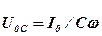и (7)

Первый из них совпадает c направлением вектора, соответствующего току, а второй и третий повернуты на углы + p/2 и - p/2, относительно тока. При сложении этих векторов получается результирующий вектор, длина которого дает амплитуду приложенного напряжения U₀, а угол j - разность фаз напряжения и тока.

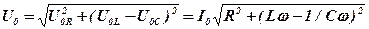. (8)

Отсюда получим выражение для силы тока

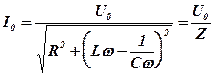(9)

Величина 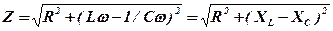называется полным сопротивлением (импедансом) цепи, X_L = Lw – индуктивным сопротивлением, X_C = 1/Сw – емкостным сопротивлением, а X = Lw - 1/Сw - реактивным сопротивлением цепи. Это выражение представляет собой закон Ома для данной цепи, поскольку связывает амплитудные значения тока и напряжения постоянным коэффициентом Z (при постоянных R, L, C и w).

Сдвиг фаз между током и напряжением также определяется из векторной диаграммы:

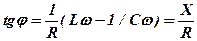. (10)

Анализ выражений (9) и (10) показывает, что частоту w (при постоянных значениях L и C) можно подобрать так, чтобы индуктивное и емкостное сопротивления были одинаковыми:

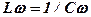. (11)

При этом реактивное сопротивление X цепи обращается в нуль, полное сопротивление Z минимально и равно только активному сопротивлению (Z = R), сила тока и напряжение совпадают по фазе (j = 0), амплитуда силы тока I₀ достигает максимальной величины:

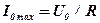. (12)

При этих условиях амплитудные значения напряжений на емкости и индуктивности противоположны по фазе и равны по величине

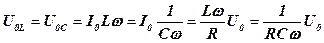
и, поэтому это явление называется резонансом напряжений (на индуктивности и емкости), а частота w_рез, при которой достигается резонанс - резонансной частотой. Она находится из соотношения(11):

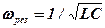. (13)

Период колебаний тока и напряжений при резонансе .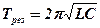

Поскольку напряжения на индуктивности и емкости изменяются в противоположных фазах, то суммарное напряжение на участке индуктивность-емкость равно нулю, хотя напряжения на индуктивности и емкости по отдельности могут быть весьма значительными и даже большими, чем напряжение на концах всей цепи.

Действительно, если Lw = 1/Cw > R, то, как следует из выражения (11), U_0L = U_0C > U₀, что может быть опасным для цепи.

Условие резонанса может быть достигнуто разными способами:

1) подбором частоты w при постоянных значениях L и C;

2) подбором индуктивности L при постоянных значениях w и C;

3) подбором емкости C при постоянных значениях w и L.

Зависимость амплитуды силы тока I₀ от частоты w графически изображена на рисунке 4. Представленные кривые называются резонансными. Чем меньше активное сопротивление R, тем круче и острее кривая, а чем больше R, тем кривая более пологая.

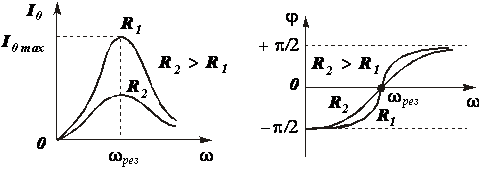
Рис. 4 Рис. 5

Зависимость сдвига фаз j от частоты w графически изображена на рисунке 5, где приведены две кривые для разных значений активного сопротивления R. При частотах w<w_рез сдвиг фаз j < 0, т.е. в цепи преобладает емкостное сопротивление. При w> w_рез сдвиг фаз j > 0, и в цепи преобладает индуктивное сопротивление. При резонансе (w = w_рез) величина j = 0.

Все рассмотренные соотношения справедливы и для действующих значений I и U, так как последние отличаются от амплитудных только постоянным множителем. Например, для гармонически изменяющихся величин I = I₀ / и U = U₀ /.