Расчет железобетонных элементов при действии продольных сил

Ранее нами рассматривались железобетонные элементы, в которых продольная сила отсутствовала, т.е. элемент подвергался только действию изгибающих моментов. В чистом виде такое напряженное состояние достаточно редко. Рассмотрим поведение железобетонных элементов при действии продольных сил. Для этого нам не потребуется вводить какие-либо изменения в нашу модель – будем устанавливать значение продольной силы равной не нулевому значению, а выбранной величине.

При исследовании изгибаемых железобетонных элементов одними из основных параметров для нас являлись кривизна элемента и его прогиб, вычисленный при данной кривизне. Для сжатых и растянутых элементов наиболее ценной информацией является прочность сечения, поэтому в нашем исследовании будем строить не диаграмму момент-кривизна, как ранее, а диаграмму продольная сила - предельный изгибающий момент. В этом случае прочность элемента обеспечена, если расчетное сочетание продольной силы и изгибающего момента находится внутри области ограниченной диаграммой и, соответственно, не обеспечена, если расчетное сочетание выходит за область диаграммы.

Построим данную диаграмму для сечения 40х60см, армированного 2-мя стержнями диаметром 25мм у каждой из боковых граней.

Для начала определим максимальное значение продольной силы, возможное для нашего сечения – естественно данное значение будет при центральном сжатии, т.е. при значении изгибающего момента равном нулю.

Значение предельной продольной силы составляет 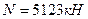. Как видим, при этом наше сечение является равномерно сжатым.

Для построения диаграммы будем менять продольную силу с шагом приблизительно 1/20 от максимального значения, т.е. по 250кН.

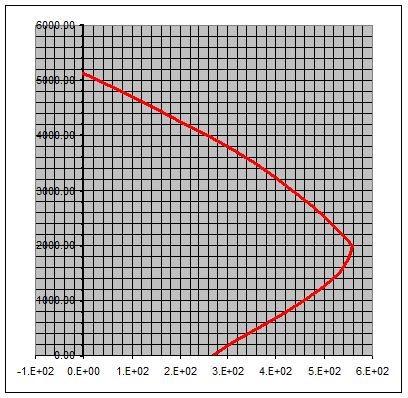
Как видно из диаграммы, при нулевой продольной силе элемент способен воспринимать некоторый момент, т.е. в данном случае элемент соответствует изгибаемому. При дальнейшем увеличении продольной силы увеличивается и предельный элемент для сечения, т.е. При некотором увеличении продольной силы можно повысить прочность изгибаемого элемента. Иногда это кажется парадоксальным, однако вспомним, что прочность нашего изгибаемого элемента исчерпывалось с достижениями напряжений в растянутой зоне предела текучести при растяжении, поэтому внешняя сжимающая сила позволяет частично компенсировать это растяжение и прочность элемента увеличивается. При дальнейшем нагружении продольной силой растянутая зона исчезает совсем и прочность на действие изгибающего момента вновь снижается. Эти два участка работы называют соответственно, случаем больших эксцентриситетов (т.е. при малой продольной силе) и случай малых эксцентриситетов (при большой продольной силе). Естественно, что при максимальной продольной силе предельный изгибающий момент равен нулю (т.е. сечение сжато равномерно).

Добавим дополнительно два стержня в средней зоне элемента, т.е. общее армирование элемента предусмотрим шестью арматурными стержнями и построим диаграмму момент-продольная сила.

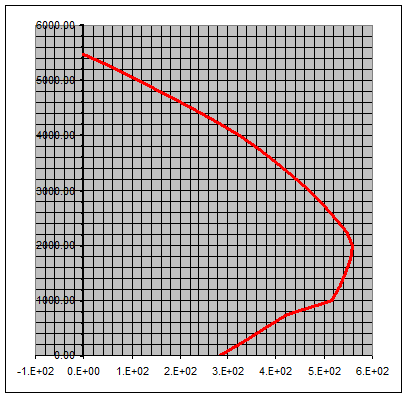
Как видно из диаграммы, на участке соответствующем случаю больших эксцентриситетов появилась некоторая неровность, т.е. выгиб. Этот выгиб соответствует наступлению текучести арматурных стержней средней зоны, в остальном характер диаграммы остался неизменным.

Совместим две полученные диаграммы на одном графике.

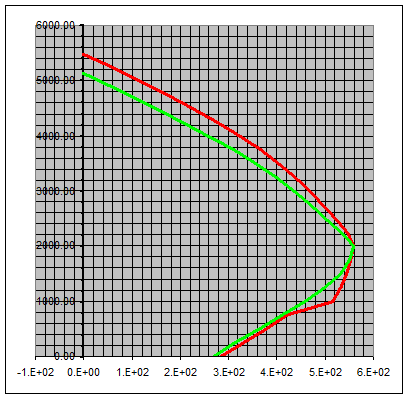
Рисунок 3‑14. Диаграмма несущей способности внецентренно-сжатого элемента

Из диаграммы видно, что граница между случаем больших и малых эксцентриситетов не зависит от наличия стержней в средней зоне, а само наличие данных стержней практически не оказывает влияния на предельный изгибающий момент при отсутствии продольной силы, но весьма сильно сказывается на предельной продольной силе при отсутствии изгибающего момента, т.е. для элементов близких к центрально сжатым добавление стержней в средней зоне столь же эффективно, как и добавление стержней в угловых зонах элемента.